Question

A uniform current carrying ring of mass m and radius R is connected by massless string as shown in figure. A uniform magnetic field $B_0$ exists in the region to keep the ring in horizontal position, then the current I in the ring is (l is the length of the string):

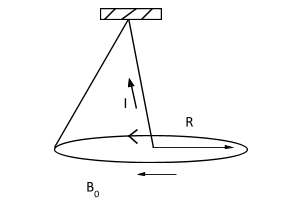
A) $\dfrac{{mg}}{{\pi R{B_0}}}$
B) $\dfrac{{mg}}{{R{B_0}}}$
C) $ - \dfrac{{mg}}{{3\pi R{B_0}}}$
D) $\dfrac{{mg}}{{\pi {R^2}{B_0}}}$

Answer 1

Hint:Torque in a magnetic field is given by:
$\mathop \tau \limits^ \to = \mathop {(IA)}\limits^ \to \times \mathop B\limits^ \to $ (I is the current, A is the area of the ring and B is the magnetic field)
Torque in a linear motion is given by:
$\tau = m \times g \times R$ (m is the mass, g is the gravitational constant and R is the radius of the ring)
Using the above two relations we will solve the problem.

Complete step by step solution:
Torque due to the magnetic field has application in electric motors. In motors current carrying conductors is placed in the magnetic ( rotor of the motor), which moves when a torque is exerted due to the magnetic field produced because of current carrying conductors of the rotor placed at an infinite distance. Torque produced will be maximum when perpendicular to the magnetic field and becomes almost zero when acts parallel to the conductors.
Torque due to the magnetic field is:
$\mathop \tau \limits^ \to = \mathop \mu \limits^ \to \mathop { \times B}\limits^ \to $($\mu $ = IA)
As magnetic field and IA are vector quantities:
$\mathop \mu \limits^ \to = \mathop k\limits^ \wedge \mu $ and $\mathop B\limits^ \to = \mathop i\limits^ \wedge {B_0}$. .................1
Torque due to the weight of the string:
$\tau = m \times g \times R$
In an equilibrium position both the torques will balance each other:
$m \times g \times R$$ = \mathop \mu \limits^ \to \mathop { \times B}\limits^ \to $
$ \Rightarrow m \times g \times R = I \times A \times {B_0} \times \mathop i\limits^ \wedge \times \mathop k\limits^ \wedge $(from equation 1)
$
   \Rightarrow m \times g \times R = I \times A \times {B_0} \\
   \Rightarrow \dfrac{{mgR}}{{A{B_0}}} = I \\
 $( i $ \times $ k =1)
Area of circle is $\pi $R², substituting value of area.
$
   \Rightarrow \dfrac{{mgR}}{{\pi {R^2}{B_0}}} = I \\
   \Rightarrow I = \dfrac{{mg}}{{\pi R{B_0}}} \\
 $ (cancelling R from denominator and numerator)

Option 1 is correct.

Note:To find the direction of force, magnetic field and current on a conductor, Fleming’s left hand rule is used. Galvanometer(small current carrying device), voltmeters, ammeters uses the concept of torque due to magnetic field and can be found out by Fleming’s left hand rule.