Question

A tree 12 m high, is broken by the wind in such a way that its top touches the ground and makes an angle ${{60}^{\circ }}$ with the ground. At what height from the bottom the tree is broken by the wind?
(a) 5.569 m
(b) 1.732 m
(c) 5.916 m
(d) 2.456 m

Answer 1

Hint: Assume a variable x which represents the height from the bottom of the tree at which the tree is broken. Since the total height of the tree is 12 m, the length of the remaining part is 12 – x. We have a trigonometric function sin which is the ratio of length of perpendicular and the hypotenuse of a right triangle. Use this sin function to solve this question.

Complete step-by-step answer:

Before proceeding with the question, we must know all the formulas that will be required to solve this question.
In a right angle triangle ABC, for the angle x, we have,

$\sin x=\dfrac{AB}{AC}$ . . . . . . . . . . . . . . . . (1)
In the question, we are given a 12 m high tree that is broken by the wind in such a way that its top touches the ground and makes an angle ${{60}^{\circ }}$ with the ground. We are required to find the height from the bottom at which the tree is broken by the wind.
Let us assume B is the bottom of the tree and the tree is broken at the point A. Also, let us assume that C is the top of the tree that is touching the ground. Since the top is making an angle ${{60}^{\circ }}$ with the ground, we can say that $\angle ACB={{60}^{\circ }}$.

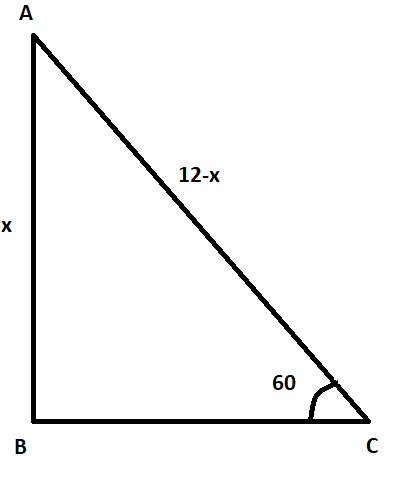
Let us assume that the tree is broken at the height x from the bottom. So, AB = x. Since the tree was 12 m height, we can say the remaining part of the tree i.e. AC = 12 – x. Using formula (1), we can say,
$\sin {{60}^{\circ }}=\dfrac{AB}{AC}$
From trigonometry, we know that $\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$ . Also, AB = x and AC = 12 – x. Substituting these in the above equation, we get,
$\begin{align}
  & \dfrac{\sqrt{3}}{2}=\dfrac{x}{12-x} \\
 & \Rightarrow \sqrt{3}\left( 12-x \right)=2x \\
 & \Rightarrow 12\sqrt{3}-\sqrt{3}x=2x \\
 & \Rightarrow x\left( 2+\sqrt{3} \right)=12\sqrt{3} \\
 & \Rightarrow x=\dfrac{12\sqrt{3}}{2+\sqrt{3}} \\
\end{align}$
Since $\sqrt{3}=1.732$, we get,
$\begin{align}
  & x=\dfrac{12\left( 1.732 \right)}{2+1.732} \\
 & \Rightarrow x=5.569 \\
\end{align}$
Hence, the answer is option (a).

Note: In the question, there are two options that are close to the answer obtained. There is a possibility that one may select the wrong one in a hurry to solve the question. So, one must be careful while marking the option.