Question

A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5cm and 13cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy if the total height of the toy is 30 cm.

Answer 1

Hint: Find the curved surface area using formula $2\pi rh$ of cylinder, $\pi r\sqrt{{{l}^{2}}+{{r}^{2}}}$ of cone, $2\pi {{r}^{2}}$ of hemisphere and add it to get the final sum and the desired result.

Complete step by step solution:
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. So the toy will look like,

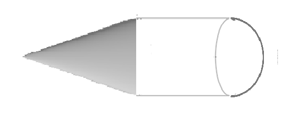
We are given a total height toy which is 30cm, so we have to find the height of the cone.
As we know the height of the cylinder is 13cm, the height of the hemisphere is 5cm as its radius and its height are the same. So, the height of cone is,
(30-5-13)cm=12cm
Now to find the area of the toy we have to find the curved surface area of all the solids which are cone, cylinder and hemisphere.
The curved surface area of the hemisphere is$2\pi {{r}^{2}}$where r is the radius.
Therefore, the curved surface area of hemisphere is,
$2r{{\left( 5 \right)}^{2}}=50rc{{m}^{2}}.........(i)$
Now the curved surface area of cone is $\pi r\sqrt{{{l}^{2}}+{{r}^{2}}}$ where ‘l’ is the slant height and r is radius.
So, the curved surface area of cone is,
$=\pi \left( 5 \right)\sqrt{{{12}^{2}}+{{5}^{2}}}=65\pi c{{m}^{2}}........(ii)$
Now the curved surface area of the cylinder is $2\pi rh$ where ‘h’ is the height of the cylinder and ‘r’ is radius.
So, the curved surface area of cylinder is,
$=2r\left( 5 \right)\left( 13 \right)=130rc{{m}^{2}}.............(iii)$
So the total area is:
Curved surface area of cone + curved surface area of hemisphere + curved surface area of cylinder
Substituting values from equation (i), (ii) and (iii), we get
$=\left( 65\pi +50\pi +130\pi \right)c{{m}^{2}}$
$=245\pi c{{m}^{2}}$
Now know that,
$\pi =\dfrac{22}{7}$
Substituting this in the total area, we get
$245\times \dfrac{22}{7}=770c{{m}^{2}}$
Hence, the total area of the toy is 770 sq.cm.

Note: Students get confused about the formulas of curved surfaces. But they have to learn all the formulas by heart. They should also be careful about the calculations as there are high chances to make mistakes in them. Students generally make mistakes in calculating the height of the hemisphere part. Drawing diagrams is important in these kinds of questions.