Question

A thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the upper half, and a charge –Q is uniformly distributed along the lower half, as shown in the Fig.1.147. The electric field E at P the centre of the semicircle is

\[\begin{align}
  & a.\,\dfrac{Q}{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}} \\
 & b.\,\dfrac{2Q}{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}} \\
 & c.\,\dfrac{4Q}{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}} \\
 & d.\,\dfrac{Q}{4{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}} \\
\end{align}\]

Answer 1

Hint: To find the expression for the electric field at a point due to the bent thin glass rod, we will consider the small portion of the rod. Then, we will compute the charge and the electric field due to that charge of the small portion of the rod, finally, we will integrate the equation of the change in the electric field.

Complete step by step solution:
Consider a small portion of the thin glass rod that is bent into a semicircle of radius r.

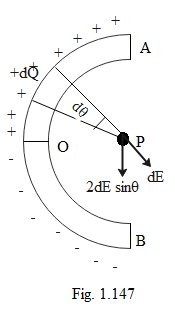
Similarly consider the portion in the case of “-dQ”.
Consider the small charge,
\[\begin{align}
  & dQ=(rd\theta )\dfrac{Q}{\left( {}^{\pi }/{}_{2}r \right)} \\
 & \Rightarrow dQ=\dfrac{2Qd\theta }{\pi } \\
\end{align}\]
The electric field due to the small charge at \[\theta \]is, \[2\,dE\sin \theta \].
Substitute the expression for the small electric field.
\[\begin{align}
  & dE=2\dfrac{dQ}{{{r}^{2}}}\sin \theta \\
 & dE=2\dfrac{2Qd\theta }{\pi {{r}^{2}}}\sin \theta \\
\end{align}\]
Now the electric field at the point P is,
\[\begin{align}
  & E=\int\limits_{0}^{{}^{\pi }/{}_{2}}{dE} \\
 & \Rightarrow E=\dfrac{4Q}{\pi {{r}^{2}}}\int\limits_{0}^{{}^{\pi }/{}_{2}}{\sin \theta \,d\theta } \\
 & \Rightarrow E=\dfrac{4}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{\pi {{r}^{2}}}\left[ -\cos \theta \right]_{0}^{{}^{\pi }/{}_{2}} \\
 & \therefore E=\dfrac{Q}{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}} \\
\end{align}\]
\[\therefore \]The expression for the electric field E at P the center of the semicircle, is \[\dfrac{Q}{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}}\], thus, the option (a) is correct.

Additional information:
While computing the value of the electric field considering the small portion, we have considered twice the value of the change in the charge, this is because, while explaining, we have considered the positive charge only, whereas, we need to consider the negative charger as well. There is no change in the value of the electric field in the case of both positive and negative charge, as the magnitude remains the same.

Note: The expression for the magnetic field due to the charge should be known to solve this problem. There will be no change in the value of the electric field in the case of both positive and negative charge, as the magnitude remains the same.