Question

A tangent to the parabola ${{x}^{2}}=4ay$ meets the hyperbola $xy={{k}^{2}}$ in two points P and Q, find the locus of the mid-point of PQ.

Answer 1

Hint: To solve this question, we should find the general equation of the tangent to the parabola ${{x}^{2}}=4ay$. Let the equation be $y=mx+c$. Substituting $y=\dfrac{{{x}^{2}}}{4a}$ in the equation $y=mx+c$ and we get a quadratic equation in x. For the line to be a tangent, we know that the quadratic equation should have only one root which implies that discriminant is zero. After getting the general equation of the tangent, we should find the solution of the tangent and the parabola $xy={{k}^{2}}$. The midpoint of the line joining points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $C\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$. We should get the sum of the roots of the solution of the tangent and the hyperbola and by removing the parameter m, we get the locus of the mid-point.

Complete step-by-step answer:
Let the equation of tangent be $y=mx+c$. Let us solve the tangent and the parabola ${{x}^{2}}=4ay$.
$\begin{align}
  & {{x}^{2}}=4a\left( mx+c \right) \\
 & {{x}^{2}}-4amx-4ac=0 \\
\end{align}$
We know that the condition for the single root of $a{{x}^{2}}+bx+c=0$ is
 $\begin{align}
  & {{b}^{2}}-4ac=0 \\
 & {{b}^{2}}=4ac \\
\end{align}$
Using this relation, we get
$\begin{align}
  & {{\left( -4am \right)}^{2}}=4\times 1\times \left( -4ac \right) \\
 & 16{{a}^{2}}{{m}^{2}}=-16ac \\
 & c=-a{{m}^{2}} \\
\end{align}$
The general equation of the tangent is $y=mx-a{{m}^{2}}$
Using this equation and solving the tangent and the hyperbola to get the points P and Q.
Solving $y=mx-a{{m}^{2}}$ and $xy={{k}^{2}}$
$\begin{align}
  & x\times \left( mx-a{{m}^{2}} \right)={{k}^{2}} \\
 & m{{x}^{2}}-a{{m}^{2}}x-{{k}^{2}}=0 \\
\end{align}$
The roots of the above equation ${{x}_{1}},{{x}_{2}}$ are the x-coordinates of the points P and Q.
We know that the formulae for sum of the roots of $a{{x}^{2}}+bx+c=0$ is $sum=\dfrac{-b}{a}$
The sum of the roots ${{x}_{1}}+{{x}_{2}}$ of the equation is ${{x}_{1}}+{{x}_{2}}=\dfrac{-\left( -a{{m}^{2}} \right)}{m}=am$
The midpoint of the line joining points $P\left( {{x}_{1}},{{y}_{1}} \right),Q\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $C\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
The x-coordinate of the mid-point of the line segment PQ is given by
${{C}_{x}}=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}=\dfrac{am}{2}$
From the equation of the tangent, the y-coordinates of P and Q can be written as
${{y}_{1}}=m{{x}_{1}}-a{{m}^{2}}$
${{y}_{2}}=m{{x}_{2}}-a{{m}^{2}}$
Adding the two equations, we get
${{y}_{1}}+{{y}_{2}}=m{{x}_{1}}-a{{m}^{2}}+m{{x}_{2}}-a{{m}^{2}}=m\left( {{x}_{1}}+{{x}_{2}} \right)-2a{{m}^{2}}$
By substituting ${{x}_{1}}+{{x}_{2}}=am$, we get
${{y}_{1}}+{{y}_{2}}=m\times am-2a{{m}^{2}}=a{{m}^{2}}-2a{{m}^{2}}=-a{{m}^{2}}$
The y-coordinate of the mid-point of the line segment PQ is given by
${{C}_{y}}=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}=\dfrac{-a{{m}^{2}}}{2}$
The point C is given by $C=\left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{am}{2},\dfrac{-a{{m}^{2}}}{2} \right)$
$\begin{align}
  & {{x}_{1}}=\dfrac{am}{2} \\
 & m=\dfrac{2{{x}_{1}}}{a} \\
\end{align}$
Using this in y-coordinate, we get
$\begin{align}
  & {{y}_{1}}=\dfrac{-a}{2}{{\left( \dfrac{2{{x}_{1}}}{a} \right)}^{2}}=\dfrac{-a}{2}\times \dfrac{4{{x}_{1}}^{2}}{{{a}^{2}}}=-\dfrac{2{{x}_{1}}^{2}}{a} \\
 & {{y}_{1}}=-\dfrac{2{{x}_{1}}^{2}}{a} \\
\end{align}$
The locus of the mid-point is
 $\begin{align}
  & y=-\dfrac{2{{x}^{2}}}{a} \\
 & {{x}^{2}}=-\dfrac{ay}{2} \\
\end{align}$
$\therefore $ The locus of the mid-point is ${{x}^{2}}=-\dfrac{ay}{2}$

Note: The important point to note is that the locus of the mid-point is not depending on the value of k. For a given value of a and slope m, the mid-point is the same for different values of k. An example of it is shown in the below figures.

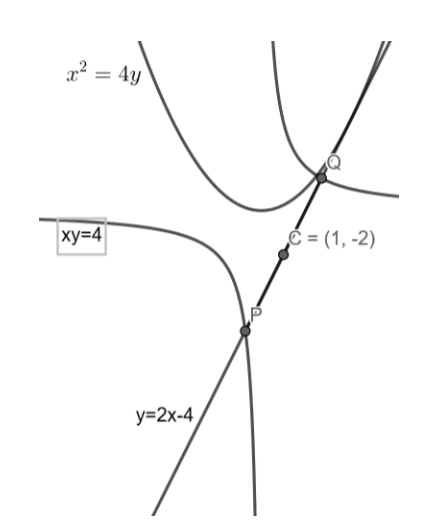
From the two figures, we can see that the hyperbola is changing but the mid-point doesn’t change which shows the interdependence of the value of k.