Question

A tall building casts a shadow of $300m$ long when the sun's altitude (elevation) is${30^0}$. Find the height of the tower.

Answer 1

Hint: First we have to define what the terms we need to solve the problem are.
Since we need to find the height for the given question, we use the triangle as the right-angled triangle and the angles are ${30^0}$and a tall building that will cast a shadow of $300m$ long when the suns set happens with the altitude of elevations.
Formula used:
By the right-angle triangle formula we knew that $\tan \theta = \dfrac{{opposite}}{{adjacent}}$(equals the hypotenuse)

Complete step by step answer:

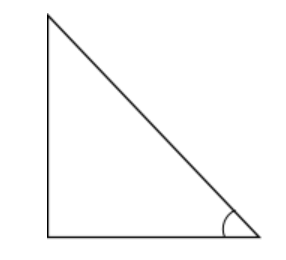
Since it is an right angled triangle let from the given diagram we clearly see that $\vartriangle ABC$be the right angled triangle where else the angles are given as below with $\angle B = {90^0}$(right angled triangle center point)and also $\angle C = {30^0}$and now fix the unknown values as X so that after applying the formula we can able to find the height as well;
Hence by the right-angle triangle formula we knew that $\tan \theta = \dfrac{{opposite}}{{adjacent}}$(equals the hypotenuse)
Which means $\tan \theta = \dfrac{{opposite}}{{adjacent}} = \dfrac{{AB}}{{BC}}$(AB is the opposite side and the adjacent side is BC which is below to the angle point) and since the degree of the angle is thirteen degree further solving, we get
$\tan \theta = \dfrac{{AB}}{{BC}} \Rightarrow \tan {30^0} = \dfrac{x}{{300}}$(The angel is thirty and X is the unknown in opposite side and the adjacent side is three hundred meters)
Therefore, tan of thirty degree is one by the square root of three and resultant
$ \Rightarrow \tan {30^0} = \dfrac{x}{{300}} \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{x}{{300}}$Now cross multiplying we get $ \Rightarrow \sqrt 3 x = 300$
Hence solving further, we get $ \Rightarrow \sqrt 3 x = 300 \Rightarrow x = 100\sqrt 3 $(taking the common term as root three and the cancel it each other)
Hence the height of the required tower is $100\sqrt 3 $ from the given tall building casts a shadow of $300m$ long when the sun's altitude (elevation) is ${30^0}$.

Note: We used the right-angled triangle formula to derive the diagram, with the angle point of thirteen and center point with respect to right angle trample is ninety degree.
Formula for the right angle triangle is HYP equals the OPP side and divides the ADJ side.