Question

A swimmer wishes to cross a 500m wide river flowing at 5$Km/h$ . Its speed with respect to water is 3$Km/h$ . It he heads in a direction making an angle$\theta $ with the flow, the time he takes to cross the river and shortest possible time to cross the river is
A. $\dfrac{{15\min }}{{\cos \theta }},10\min $
B. $\dfrac{{15\min }}{{\sin \theta }},10\min $
C. $\dfrac{{10\min }}{{\sin \theta }},10\min $
D. $\dfrac{{10\min }}{{\cos \theta }},10\min $

Answer 1

Hint: Since the velocity of the river is constantly changing, we have to consider the relative velocity of the swimmer with respect to that of the river. The velocities cannot be added or subtracted directly, since they are not in parallel direction but at an angle of $\theta $. Hence, the velocity of the river must be resolved into horizontal and vertical components.

Complete step by step answer:
There are two parts in the question to answer.
First the time taken by him to cross
And second, also the shortest possible time to cross the river channel.
We are given; A swimmer wishes to cross a 500m wide river flowing at 5$Km/h$
Let us consider the diagram for better understanding.

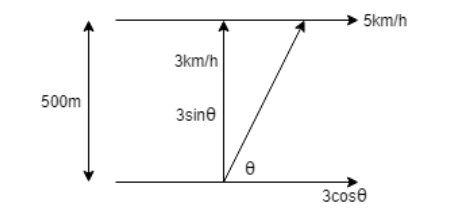
Here the swimmer heads in a direction making an angle$\theta $ with the flow and two components of sin and cos are there. He wished to cross along the sin component.
So, the vertical component $3\sin \theta $ will take him to his desired place
Here distance is 500m or 0.5km (in standard terms)
Velocity is $3\sin \theta $
Now we know the formula of time which is $\dfrac{{dis\tan ce}}{{speed}}$ ……… (1)
Therefore, time T $=\dfrac{{0.5}}{{3\sin \theta }}$ , which is equal to $\dfrac{{10\min }}{{\sin \theta }}$ ……… (2)
Here we have solved the one part of the question.

Now we need to know the time taken by him to cross the stream.
${V_s}$ Is the speed of swimmer which is 3$Km/h$
Then again using the formula for time from equation 1 we get T(time) $=\dfrac{d}{{{V_s}\sin \theta }}$ , where d is the distance.
In general the angle between the stream and the path swimmer will follow will have ${90^0}$
Hence sin ${90^0}$=1
Substituting the value, $T=\dfrac{{0.5km}}{{3 \times 1}}$ , on solving it and converting it to standard unit hour we will get T equal to 10min ……. (3)
Hence, combining the result of equation (1) and (3) the time he takes to cross the river and shortest possible time to cross the river is $\dfrac{{10\min }}{{\sin \theta }}$, 10min

Hence, the correct answer is option (C).

Note: Whenever such a question occurs, where there is a chance to make a diagram, must make it as it clarifies the situation and gives a solution. In the following diagram we are able to understand that the swimmer wants to go along sine function. Always represent the standard units and convert wherever it needs.