Question

A survey shows 63% of Indians like mangoes whereas 76% like apples. If x % of the Indians like both mangoes and apples then,
(a) $x=39$
(b) $x=63$
(c) $39\le x\le 63$
(d) None of these

Answer 1

Hint: In order to solve this problem, we need to identify the terms that include the intersection of two events and terms that include the union of two terms. We here have to assume that all the Indians at least choose mangoes or apples. The formula that will be used to solve this problem is as follows, $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$ where, $n\left( A \right)$ and $n\left( B \right)$ are two spate events.

Complete step by step answer:
We are given that Indians that like mangoes are 63% and Indians that like apples are 76%.
Let x % of Indians like both mangoes and apples.
As the numbers are given in percentage, it is assumed that all the Indians either like mangoes or apples.
Let the event where Indians like mangoes be $n\left( A \right)$ , and let the event where Indians like apples be the event $n\left( B \right)$ .
As we know that all the Indians either like apples or mangoes $n\left( A\cup B \right)=100................(i)$
Let the event where Indians like both mangoes and oranges be $n\left( A\cap B \right)$ .
We can show the events with the help of venn diagram as follows,

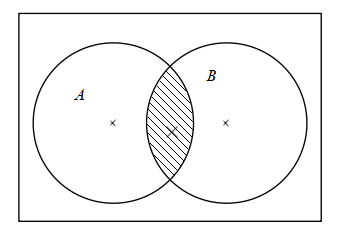
As we can see that the shaded region shows the intersection of A and B that is the Indians who like both mangoes and oranges.
Here, $A\cup B$ shows that either A or B is correct which include all the Indians and $A\cap B$ shows both events have to be satisfied simultaneously.
To solve this, there is an identity that consists of all the terms which is as follows,
$n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right).......................(ii)$
Substituting the values, we get,
$100=63+76-n\left( A\cap B \right)$
But, $n\left( A\cap B \right)=x%$
Solving this equation further for $x\%$ we get,
$\begin{align}
  100=63+76-x \\
  \Rightarrow x=39\% \\
\end{align}$
Therefore, the Indians that like both mangoes and apples are 39%.
Hence the correct option is (a).

Note:
The common mistake here that is done is, the signs of intersection are interchanged with the union which give the wrong answer. We can remember as the union is represented by “U” and the other one is the symbol of the intersection. The assumption that all the Indians like either apples or mangoes is very important to solve this problem.