A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of \[30^\circ\], which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be \[60^\circ \]. Find the time taken by the car to reach the foot of the tower from this point.
Answer
Verified259.7k+ views
Hint: Solve by representing the text with a diagram, then use trigonometric formulas to find the relation between the given variables. Use formula for speed in terms of distance and time to get the time taken by the car to reach the foot of the tower from the given point.
Let us represent the scenario with a diagram.
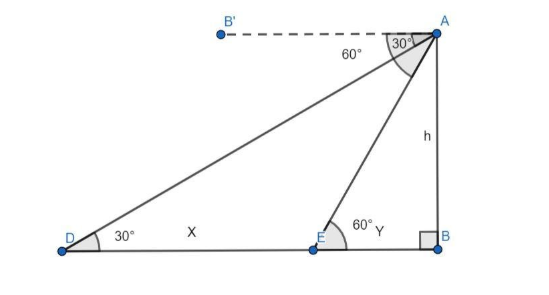
Let AB be the tower with the man standing on the top of the tower at A. Let D be the point when the angle of depression is \[30^\circ \] and E be the point where the angle of depression is \[60^\circ \].
Let line segment DE be equal to X and line segment EB be equal to Y.
Let the speed of the car be \[v\], which is a constant since the car travels with a uniform speed.
We know that distance covered is speed times time, that is:
\[d = v \times t{\text{ }}............{\text{(1)}}\]
where \[d\] is the distance covered, \[v\] is the speed and \[t\] is the time taken.
The car takes 6 seconds to go from D to E.
Hence, using equation (1), we obtain the value of X as follows:
\[X = v \times 6\]
\[X = 6v{\text{ }}...........{\text{(2)}}\]
Consider \[\Delta ADB\], we know that tangent of an angle is the ratio of opposite side by adjacent side, therefore we have:
\[\tan \angle ADB = \dfrac{{AB}}{{DB}}\]
\[\tan 30^\circ = \dfrac{h}{{X + Y}}\]
Using \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\], we get:
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{X + Y}}\]
Cross multiplying, we have:
\[X + Y = \sqrt 3 {\text{ }}h{\text{ }}............{\text{(3)}}\]
Similarly, consider \[\Delta AEB\] and applying tangent formula to \[\angle AEB\] , we have:
\[\tan \angle AEB = \dfrac{{AB}}{{EB}}\]
\[\tan 60^\circ = \dfrac{h}{Y}\]
Using \[\tan 60^\circ = \sqrt 3 \] , we get:
\[\sqrt 3 = \dfrac{h}{Y}\]
\[h = \sqrt 3 {\text{Y }}..........{\text{(4)}}\]
Now, substituting equation (4) in equation (3), we get:
\[X + Y = \sqrt 3 \left( {\sqrt 3 Y} \right)\]
\[X + Y = 3Y\]
Solving for \[Y\] in terms of \[X\] , we get:
\[X = 3Y - Y\]
\[X = 2Y\]
\[Y = \dfrac{X}{2}\]
Using equation (2), we get \[Y\] in terms of \[v\] .
\[Y = \dfrac{{6v}}{2}\]
\[Y = 3v{\text{ }}..........{\text{(5)}}\]
Now, let us use equation (1) to find the time calculated to reach the foot of the tower from point E.
\[t = \dfrac{d}{v}\]
Here, the distance \[d\] is \[Y\] .
\[t = \dfrac{Y}{v}\]
Using equation (5), we get the time taken as follows:
\[t = \dfrac{{3v}}{v}\]
\[t = 3{\text{ sec}}\]
Therefore, it takes 3 seconds to reach the foot of the tower from the given point.
Hence, the correct answer is 3 seconds.
Note: You might get confused with the term angle of depression. It is the angle between the
horizontal line of sight and the object from the observer. Another common mistake is to write the tangent formula wrong when substituting, for example, you might write, \[\tan \angle AEB = \dfrac{Y}{h}\], which is an error.
Let us represent the scenario with a diagram.
Let AB be the tower with the man standing on the top of the tower at A. Let D be the point when the angle of depression is \[30^\circ \] and E be the point where the angle of depression is \[60^\circ \].
Let line segment DE be equal to X and line segment EB be equal to Y.
Let the speed of the car be \[v\], which is a constant since the car travels with a uniform speed.
We know that distance covered is speed times time, that is:
\[d = v \times t{\text{ }}............{\text{(1)}}\]
where \[d\] is the distance covered, \[v\] is the speed and \[t\] is the time taken.
The car takes 6 seconds to go from D to E.
Hence, using equation (1), we obtain the value of X as follows:
\[X = v \times 6\]
\[X = 6v{\text{ }}...........{\text{(2)}}\]
Consider \[\Delta ADB\], we know that tangent of an angle is the ratio of opposite side by adjacent side, therefore we have:
\[\tan \angle ADB = \dfrac{{AB}}{{DB}}\]
\[\tan 30^\circ = \dfrac{h}{{X + Y}}\]
Using \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\], we get:
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{X + Y}}\]
Cross multiplying, we have:
\[X + Y = \sqrt 3 {\text{ }}h{\text{ }}............{\text{(3)}}\]
Similarly, consider \[\Delta AEB\] and applying tangent formula to \[\angle AEB\] , we have:
\[\tan \angle AEB = \dfrac{{AB}}{{EB}}\]
\[\tan 60^\circ = \dfrac{h}{Y}\]
Using \[\tan 60^\circ = \sqrt 3 \] , we get:
\[\sqrt 3 = \dfrac{h}{Y}\]
\[h = \sqrt 3 {\text{Y }}..........{\text{(4)}}\]
Now, substituting equation (4) in equation (3), we get:
\[X + Y = \sqrt 3 \left( {\sqrt 3 Y} \right)\]
\[X + Y = 3Y\]
Solving for \[Y\] in terms of \[X\] , we get:
\[X = 3Y - Y\]
\[X = 2Y\]
\[Y = \dfrac{X}{2}\]
Using equation (2), we get \[Y\] in terms of \[v\] .
\[Y = \dfrac{{6v}}{2}\]
\[Y = 3v{\text{ }}..........{\text{(5)}}\]
Now, let us use equation (1) to find the time calculated to reach the foot of the tower from point E.
\[t = \dfrac{d}{v}\]
Here, the distance \[d\] is \[Y\] .
\[t = \dfrac{Y}{v}\]
Using equation (5), we get the time taken as follows:
\[t = \dfrac{{3v}}{v}\]
\[t = 3{\text{ sec}}\]
Therefore, it takes 3 seconds to reach the foot of the tower from the given point.
Hence, the correct answer is 3 seconds.
Note: You might get confused with the term angle of depression. It is the angle between the
horizontal line of sight and the object from the observer. Another common mistake is to write the tangent formula wrong when substituting, for example, you might write, \[\tan \angle AEB = \dfrac{Y}{h}\], which is an error.
Last updated date: 15th Sep 2023
•
Total views: 259.7k
•
Views today: 5.59k
