Question

When a stone is tied to a string and rotated in a circular motion, the tension produced in the string is due to:

A. Centripetal force
B. Centrifugal force
C. Pseudo force
D. None of these

Answer 1

Hint: When an object is rotating in a circle its direction of velocity keeps on changing. When velocity changes there will be an acceleration and this contributes for the force. In this case too the same force will be acting in the string.

Complete answer:
According to Newton's second law the rate of change of momentum of the body will be equal to the external force acting on it.
In this case too when an object is moving in circular motion the direction of velocity changes at every instant.

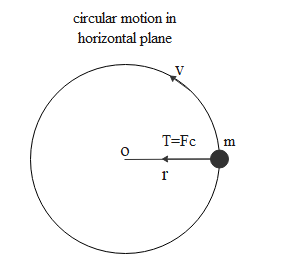
The above diagram represents the stone of mass (m) rotating in a circle or radius (r) with velocity (v) and T is the tension force and Fc is the centripetal force acting towards the center of the circle (O). The only connection to the stone is the string so, if it is performing circular motion in a horizontal circle then whatever the horizontal force it has to be present in the string. So when an object performs circular motion then along the radial direction there will be centripetal force acting. Centripetal force acts towards the center, whereas tension is a pulling force and it also will act towards the center from the stone. Hence centripetal force will provide the tension in string.
As long as the magnitude of velocity is constant, the centripetal force also will be constant. The direction of centripetal force will be always towards the center.

So, the correct answer is “Option A”.

Note:
Generally there will be a case of constant magnitude of velocity and hence centripetal force will be constant. There are some cases where magnitude of velocity depends on the time i.e speed depends on the time and it varies with time. Then centripetal force will be varying at every instant and we come across a new term called tangential acceleration.