Question

A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Also, find the maximum volume of the box thus formed.

Answer 1

Hint: To maximize a variable quantity, we first convert it and make it a function of a single variable and then we differentiate it with respect to that variable to get the value of the variable when the function gets to an extreme point.

Complete step-by-step answer:
The volume of a cuboid is
\[Volume=lbh\]
Where l=length of the cuboid
b=breadth of the cuboid
h=height of the cuboid
The volume of a cube is
\[Volume=sid{{e}^{3}}\]
As mentioned in the question, the square is cut from all the corners of the tin sheet of side 18cm.
Now, let the side of the squares cut from the corners of the sheet be ‘x’. On forming a box without a top from this sheet, we get a cuboid having length as 18-2x cm, breadth as 18-2x cm and height as x cm.

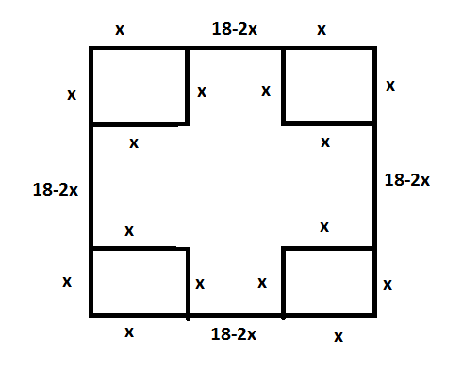
Now, on looking this figure, we can find that
The length of the cuboid is 18-2x.
The breadth of the cuboid is x.
The height of the cuboid is x.
Now, using the formula for volume of a cuboid, we get
\[V=(18-2x)(18-2x)(x)\] (Where V is the volume of the cuboid)
\[V={{(18-2x)}^{2}}x\]
\[V=(324+4{{x}^{2}}-72x)x\]
\[V=(324x+4{{x}^{3}}-72{{x}^{2}})\ \ \ \ \ ...(a)\]
Now, as we get the volume of the box thus formed on bending the side of the tin sheet which was left after the squares being taken out from it as a function of x which is the side of the squares that are taken out.
So, on differentiating the volume with respect to x, we get
\[\dfrac{dV}{dx}=\dfrac{d(324x+4{{x}^{3}}-72{{x}^{2}})}{dx}\]
\[\dfrac{dV}{dx}=324+12{{x}^{2}}-144x\]
Now, to get the value of x at which the volume of the box is maximum, we take
\[\dfrac{dV}{dx}=0\]
\[324+12{{x}^{2}}-144x=0\]
\[\begin{align}
  & 12(x-3)(x-9)=0 \\
 & (x-3)(x-9)=0 \\
 & x=3,9 \\
\end{align}\]
Now, x=9 is not possible as the side of the original square tin sheet is 18cm.
Therefore, the volume of the box is maximum when x=3 and the maximum volume of the box can be calculated using equation (a) as follows
\[\begin{align}
  & V=(324x+4{{x}^{3}}-72{{x}^{2}}) \\
 & V=(324\times 3+4\times {{3}^{3}}-72\times {{3}^{2}}) \\
 & V=(972+4\times 27-72\times 9) \\
 & V=(972+108-648)=432c{{m}^{3}} \\
\end{align}\]

Note: This process works as any function attains its maximum or minimum value at the point where its derivative becomes 0. In order to get that which value of x is maxima or minima, we need to put the different values of x that we get by equating the derivative to 0 and then check at which value of x, maxima is present and at which x minima is present.
Also, the value of x cannot be 9 because in that case the volume of the box hence formed would become 0 and it would be clearly impossible.