Question

A square is inscribed in the circle \[{{x}^{2}}+{{y}^{2}}-2x+4y-3=0\] with its sides parallel to the coordinate axes. One vertex of square is:
A. (3, 4)
B. (3, -4)
C. (8, -5)
D. (-8, 5)

Answer 1

Hint: At first, convert the equation of circle into the form \[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\] where \[\left( {{x}_{1}},{{y}_{1}} \right)\] is the center and r is radius. Then, use the property that, diagonal of a square equals the diameter of the circle to find the length of the square's side. Then, consider the coordinate of any of the vertices of the square as (a, b) and from that find other in terms of a and b. After that, use the property that the midpoint of the diagonal of the square is the center of the circle.

Complete step by step answer:
In the question, we are said that, square is drawn inside or inscribed in a circle with a given equation \[{{x}^{2}}+{{y}^{2}}-2x+4y-3=0\] with a given condition that is the sides of square parallel to the axis. For the given condition, we have to find one vertex of the square.
The given equation of circle is,
\[{{x}^{2}}+{{y}^{2}}-2x+4y-3=0\]
We will further write the equation as,
\[\begin{align}
  & {{x}^{2}}-2x+1+{{y}^{2}}+4y+4-3-5=0 \\
 & \Rightarrow {{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}-8=0 \\
\end{align}\]
So, the equation is formed as,
\[{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=8={{\left( 2\sqrt{2} \right)}^{2}}\]
If the equation of circle is in form of,
\[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\]
Then, its center is \[\left( {{x}_{1}},{{y}_{1}} \right)\] and radius is r.
As the equation is \[{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}={{\left( 2\sqrt{2} \right)}^{2}}\] so, its center is \[\left( 1,-2 \right)\] and radius is \[2\sqrt{2}\]
Let ABCD be the square inside the circle, whose center is O. So, it can be drawn as,

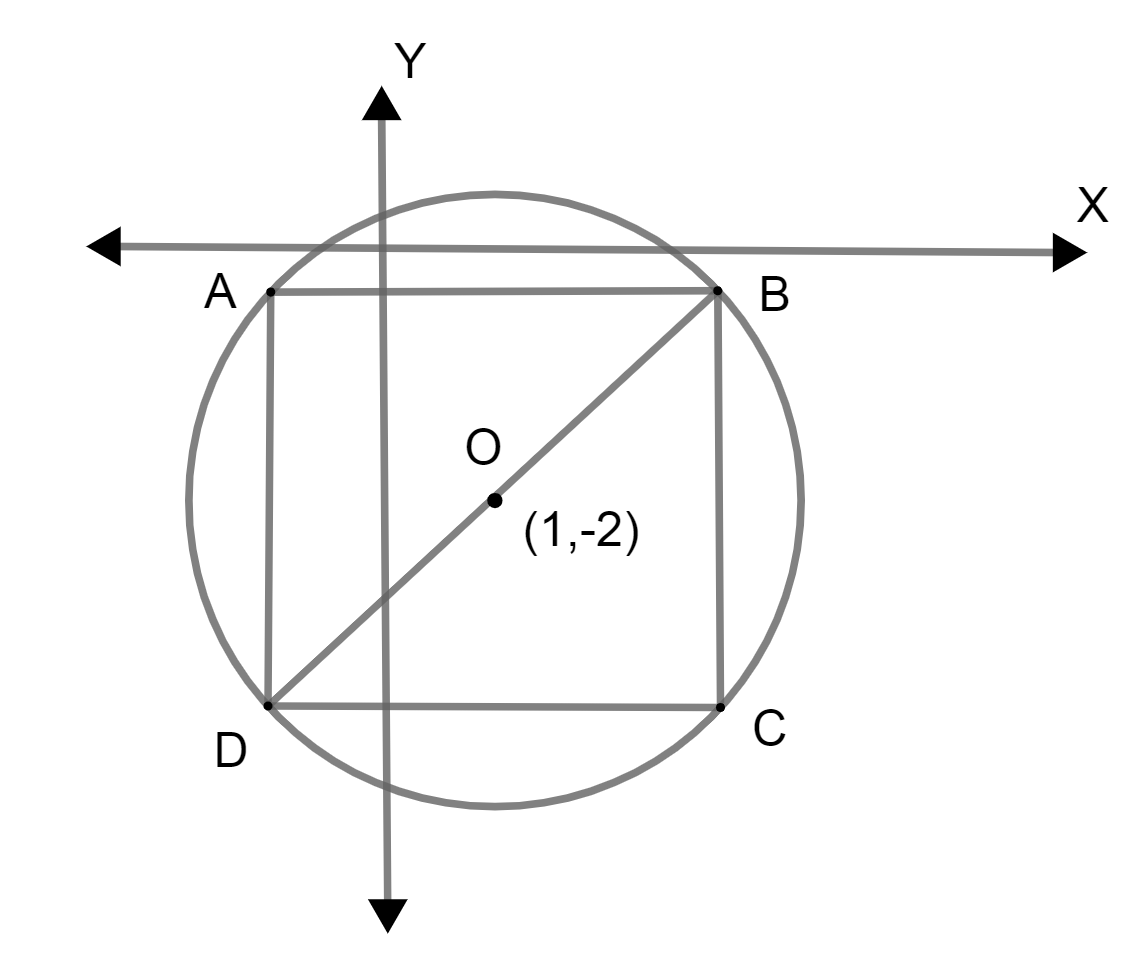
As we know that, the radius of the circle is \[2\sqrt{2}\] so, the diameter will be twice as radius \[4\sqrt{2}\].
The diameter of the circle is a diagonal of a square. Using the relation, diagonal of square \[\sqrt{2}\times \text{side of square}\] we can find the side of the square.
Here, side is AB, so, its length will be \[\dfrac{\text{diagonal}}{\sqrt{2}}\Rightarrow \dfrac{4\sqrt{2}}{\sqrt{2}}\Rightarrow 4\]
Now, let’s suppose, coordinates of B be (a, b).
Now, as we know that, each side length is 4 and sides are parallel to axes, we can write other coordinates in terms of a and b too.
So, the coordinates of A, C and D are \[\left( a-4,b \right);\left( a,b-4 \right);\left( a-4,b-4 \right)\].
We know that, midpoint of the diagonal of a square is the center of the circle. So, we can say that the midpoint of the coordinator of B and D is the center of the circle.
We will find midpoint using formula, \[x'=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\,\,and\,\,y'=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\]
If $\left( x',y' \right)$ is the midpoint between \[\left( {{x}_{1}},{{y}_{1}} \right)\,\,and\,\,\left( {{x}_{2}},{{y}_{2}} \right)\] we can find midpoint using formula, \[x'=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\,\,and\,\,y'=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\].
 Here, points are B(a, b) and D(a-4, b-4), so, its midpoint will be,
\[\left( \dfrac{a+a-4}{2},\dfrac{b+b-4}{2} \right)\Rightarrow \left( \dfrac{2a-4}{2},\dfrac{2b-4}{2} \right)\]
Now, as we also know that its midpoint is the center of the circle which is (1, -2).
So we can say,
\[\left( \dfrac{\left( 2a-4 \right)}{2},\dfrac{\left( 2b-4 \right)}{2} \right)=\left( 1,-2 \right)\]
So, we can say that,
\[\begin{align}
  & \dfrac{2a-4}{2}=1\,\,and\,\,\dfrac{2b-4}{2}=-2 \\
 & \Rightarrow 2a-4=2\,\,and\,\,2b-4=-4 \\
\end{align}\]
Thus, on simplifying we can say that,
\[\begin{align}
  & 2a=6\,\,\Rightarrow a=3 \\
 & and\,\,2b=0\,\,\Rightarrow b=0 \\
\end{align}\]
So, the coordinates of B are (3, 0).
The coordinates of A is (-1, 0), C is (3, -4) and D is (-1, -4).
Among the above coordinates only (3, -4) matches the option.

So, the correct answer is “Option B”.

Note: Students while solving the problem must know the properties of the square when inscribed in the circle just like the diameter of a circle is equal to the diagonal of the square. Also, these properties help to solve the questions more easily.