Question

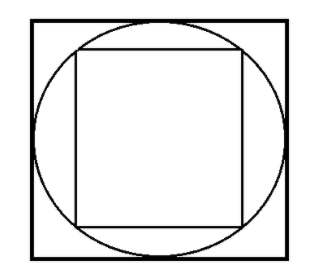
A square is inscribed in a circle of diameter $d$ and another square is circumscribing the circle. Find the ratio of the outer square to the area of the inner square.

Answer 1

Hint: In this question we can see through the diagram that the square inscribed inside the circle will its diagonal equal to the diameter of the circle, and the square circumscribing the circle will have its side equal to the diameter of the circle. So, by this we can find the ratios of the areas of these two squares.

Complete step-by-step answer:
Here in this question first of all we will enlist the given quantities and after that we will solve this question.
So, it is given in this question that
A square is inscribed in a circle and there is another square which is circumscribing the circle.
The diameter of the circle is $d$.

So now, in the given figure if we consider firstly the square which is inscribed inside the circle we can see that the diagonal of the square is equal to the diameter of the circle.
So, if we consider $s$ as the side of the square inscribed in the circle, then the diagonal of the square will be equal to $\sqrt 2 s$ (as the diagonal of the square is always $\sqrt 2 $ times its side).
Now, as we said earlier that the diagonal of the square is equal to the diameter of the circle.
It means that, $d = \sqrt 2 s$
$ \Rightarrow s = \dfrac{d}{{\sqrt 2 }}$
So, now as we know that area of a square is equal to ${\left( {side} \right)^2}$
$ \Rightarrow $Area of square (inscribed) $ = {s^2}$
$ \Rightarrow $Area of square (inscribed) $ = {\left( {\dfrac{d}{{\sqrt 2 }}} \right)^2}$
$ \Rightarrow $Area of square (inscribed) $ = \dfrac{{{d^2}}}{2}$ ……(i)
Now, if we consider the square circumscribing the circle, we observe that its side will be equal to the diameter of the circle, as by the diagram it is visible that the length of the diameter of the circle is equal to the side of the outer square.
So, now if we assume that side of the outer square is $S$
So, by above statement we can say that $S = d$
So, the area of the outer square will be equal to${\left( {side} \right)^2}$
$ \Rightarrow $Area of square (circumscribing) $ = {S^2}$
$ \Rightarrow $Area of square (circumscribing) $ = {\left( d \right)^2}$ ……….(ii)
So, in the question it is asked that we have to find the ratio of the area of the outer square to the area of the inner square.
So, from equations (i) and (ii) we know that
Area of square (inscribed) $ = \dfrac{{{d^2}}}{2}$ ……(i)
Area of square (circumscribing) $ = {\left( d \right)^2}$ .….(ii)
So, ratio of their areas will be equal to
(Area of outer circle) $ \div $(Area of inner circle)
$ \Rightarrow $Ratio$ = \dfrac{{{d^2}}}{{\left( {\dfrac{{{d^2}}}{2}} \right)}}$
$ \Rightarrow $Ratio$ = 2$

Note: In this question the extra information we needed to know was that the diagonal of the square inscribed is equal to the diameter of the circle, it means that the diagonal of the square inscribed will pass through the center of the circle. This statement can also be proved by the theorem that every right angled triangle formed inside a circle will have its hypotenuse as the diameter of the circle.