Question

A spring balance reads \[{w_1}\] when a ball is suspended from it. A weighing machine reads \[{w_2}\] when a tank containing liquid is kept on it. When the ball is immersed in the liquid, the spring balance reads \[{w_3}\] and the weighing machine reads \[{w_4}\] . Then,
(A) \[{w_1} > {w_3}\]
(B) \[{w_2} < {w_4}\]
(C) \[{w_1} + {w_2} = {w_3} + {w_4}\]
(D) \[{w_1} + {w_4} = {w_2} + {w_3}\]

Answer 1

Hint:First of all, we will draw the diagram of all the objects to show the forces including the tension forces. Then we will equate the forces and manipulate accordingly to make some comparison between them.

Complete step by step answer:
In the given question, we are supplied the following data:
The reading of the spring is \[{w_1}\] when a ball is suspended from it.
The reading of the weighing machine is \[{w_2}\] when a tank containing liquid is kept on it.
The reading of the spring is \[{w_3}\] when the ball is immersed in the liquid and the weighing machine reads \[{w_4}\] .
We are asked to find the relation between \[{w_1}\] , \[{w_2}\] , \[{w_3}\] and \[{w_4}\] .
Here, \[{w_1}\] and \[{w_3}\] are the two forces by the ball and spring onto each other before and after immersion in the liquid.
Again, we have,
\[\Rightarrow{w_2}\] and \[{w_4}\] are the two forces which are exerted by the tank and the weighing machine onto each other before and after immersion in the liquid.
Let us assume the mass of the ball be \[m\] and the mass of the tank be \[M\] accordingly. Again, let us assume the force of interaction between the ball and tank be \[N\] .
For better understanding, we draw the diagrams showing their weights and the reaction forces respectively.

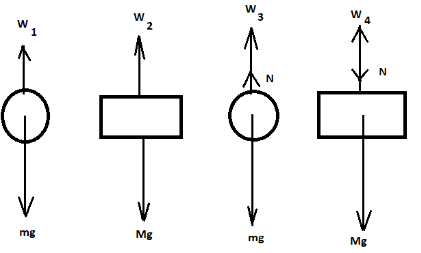
In the diagram we can see that, in the first figure, the weight of the body is balanced by the tension force in the string, which goes the same for the second figure too. In the third figure, the normal reaction force is directed upwards along the direction of the tension force. In the last figure, the normal reaction force is directed in a downward direction.
From the diagram, we can come to conclusion that:
\[\Rightarrow{w_1} = mg\] …… (1)
\[\Rightarrow{w_2} = Mg\] …… (2)
\[\Rightarrow{w_3} + N = mg\] …… (3)
\[\Rightarrow{w_4} = N + Mg\] …… (4)
On comparing the equations (1) and (3), we get:
\[\Rightarrow{w_3} + N = {w_1}\]
This clearly says that:
\[\Rightarrow{w_1} > {w_3}\]
Again, on comparing the equations (2) and (4), we get:
\[\Rightarrow{w_4} = N + {w_2}\]
This clearly says that:
\[\Rightarrow{w_2} < {w_4}\]
Hence, the result is \[{w_1} > {w_3}\] and \[{w_2} < {w_4}\] .

The correct options are A and B.

Note:This problem can only be solved if you have a good knowledge on the forces and the line of action. It is important to remember that the tension force in a spring is always directed in the upward direction and don’t get confused with that.