Question

A sphere of radius R has a charge density of $\rho \left( r \right)={{\rho }_{0}}\left( \dfrac{r}{R} \right)$ where ${{\rho }_{0}}$ is a constant and $r$ is the distance from center of the sphere. Find the electric field for $r > R$.
A. $E=\dfrac{{{\rho }_{0}}{{r}^{2}}}{4{{\varepsilon }_{0}}{{R}^{2}}}$
B. \[E=\dfrac{{{\rho }_{0}}R}{2{{\varepsilon }_{0}}}\]
C. $E=\dfrac{{{\rho }_{0}}{{R}^{3}}}{4{{\varepsilon }_{0}}{{r}^{2}}}$
D. $E=\dfrac{4{{\rho }_{0}}{{R}^{3}}}{3{{\varepsilon }_{0}}{{r}^{2}}}$

Answer 1

Hint: Gauss theorem states that the electric flux coming out of a closed surface is equal to $\dfrac{1}{{{\varepsilon }_{0}}}$ times the charge it encloses. Draw a diagram of the charge distribution and apply. Gauss theorem to find the electric field at the given point.

Complete step-by-step answer:
The given charge distribution has density: $\rho \left( r \right)={{\rho }_{0}}\left( \dfrac{r}{R} \right)$
Gauss theorem states that, the electric flux coming out of a closed surface is equal to $\dfrac{1}{{{\varepsilon }_{0}}}$times the charge it encloses. Where ${{\varepsilon }_{0}}$ is electrical permittivity of the material and flux $\phi $ is equal to:
\[\phi =\int\limits_{S}{\vec{E}.d\vec{S}}\]
Where, electric flux is known as the number of field lines perpendicular to a surface area. Therefore, in the equation above: E, the electric field on a given surface S is being used to calculate the flux $\phi $.

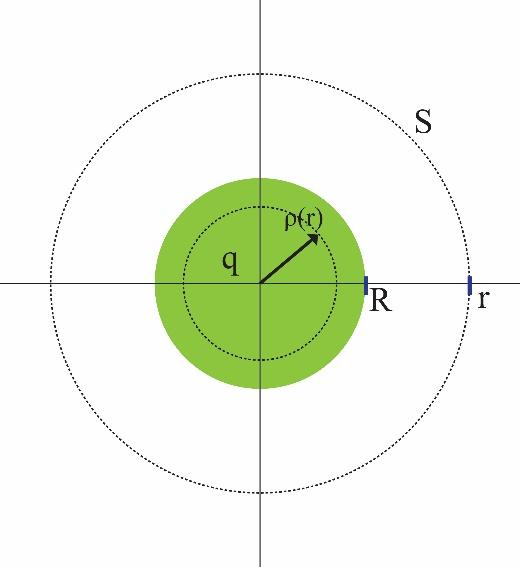
Therefore, gauss theorem can mathematically be expressed as:
$\oint\limits_{s}{\vec{E}.d\vec{s}}=\dfrac{q}{{{\varepsilon }_{o}}}$… (1)
q is the total charge enclosed in the closed surface S.
Total charge q in terms of the charge density can be expressed as:
\[q=\int{\rho dV}\]… (2)
Where, $\rho $ is the charge density and V is the volume.
Combining the equation (1) and (2) we have:
\[\oint\limits_{S}{\vec{E}.d\vec{s}}=\dfrac{\int{\rho dV}}{{{\varepsilon }_{o}}}\]… (3)
Now we have to evaluate the above integral.

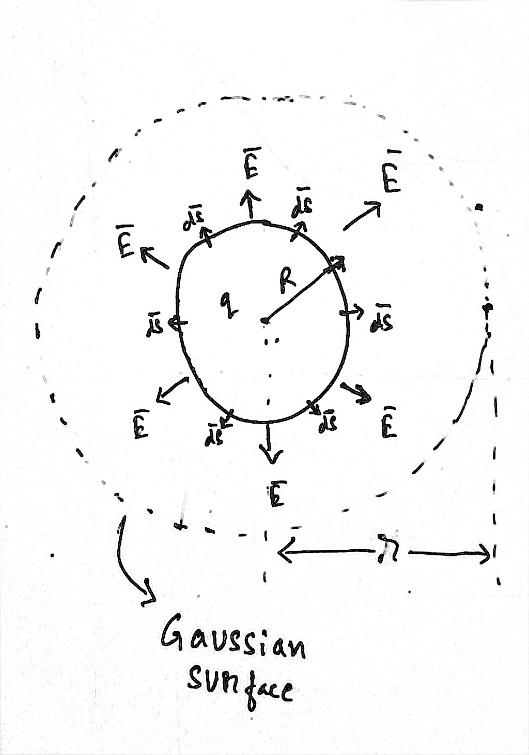
Since, it is evident from the figure that the surface S is symmetrically placed from the charged sphere. Therefore, the expression simplifies as:
\[\phi =\int\limits_{S}{\vec{E}.d\vec{S}}=\left| {\vec{E}} \right|\int\limits_{S}{\left| d\vec{s} \right|}=4\pi {{r}^{2}}E\]… (4)
As the area of the surface S is $4\pi {{r}^{2}}$.
Evaluating the total charge:
\[\begin{align}
  & q=\int{\rho dV} \\
 & q=\iiint\limits_{V}{\dfrac{{{\rho }_{0}}}{R}r\times dV} \\
 & q=\iiint\limits_{V}{\dfrac{{{\rho }_{0}}}{R}r\times {{r}^{2}}\sin \theta drd\theta d\varphi } \\
\end{align}\]
Where $\theta $ and $\varphi $ are azimuthal angles.
\[\int\limits_{\theta =0}^{\pi }{\sin \theta d\theta }=2\]
\[\int\limits_{\varphi =0}^{2\pi }{d\varphi }=2\pi \]
The total charge comes out to be:
\[\begin{align}
  & q=\dfrac{4\pi {{\rho }_{0}}}{R}\int\limits_{r=0}^{R}{{{r}^{3}}dr} \\
 & q=\dfrac{4\pi {{\rho }_{0}}}{R}\dfrac{{{R}^{4}}}{4} \\
 & q=4\pi {{\rho }_{0}}\dfrac{{{R}^{3}}}{4} \\
\end{align}\]
Evaluating the Gaussian surface integration, from equation (3) and (4), we have,
$\begin{align}
  & \oint\limits_{S}{\vec{E}.d\vec{s}}=\dfrac{q}{{{\varepsilon }_{o}}} \\
 & 4\pi {{r}^{2}}\times E=\pi {{\rho }_{0}}\dfrac{{{R}^{3}}}{{{\varepsilon }_{o}}} \\
 & \text{That is,} \\
 & E=\dfrac{{{\rho }_{0}}{{R}^{3}}}{4{{\varepsilon }_{0}}{{r}^{2}}} \\
\end{align}$
Thus, option C is the correct answer.

NOTE: We are allowed to use gauss theorem for all the charge distributions; it is not compulsory for them to be symmetric. But one should be careful while calculating the flux. That is only when the charge distribution is symmetrical, will the electric field term E and the surface area $4\pi {{r}^{2}}$ will come out of the integration independently.