Question

A source of sound is travelling at $\dfrac{{100}}{3}m/s$ along a road, towards a point $A$. When the source is $3m$ away from $A$, a person standing at a point $O$ on a road perpendicular to the track hears a sound of frequency $f$. The distance of $O$ from $A$ at that time is $4m$. If the original frequency is $640Hz$, then the value of $f$ is (given velocity of sound $ = 340m/s$)
A) $620Hz$
B) $680Hz$
C) $720Hz$
D) $740Hz$

Answer 1

Hint: When the source or the observer or both are moving with time then the frequency of the sound changes which is known as the Doppler Effect. Here, the source does not directly advance to the observer, hence you need to resolve the components and analyze accordingly.

Formula used:
If a source of sound with frequency $f$ moves with a velocity ${v_{source}}$, and the observer with a velocity ${v_{observer}}$, the observed frequency $f'$ due to the doppler effect becomes
$f' = f\left( {\dfrac{{{v_{sound}} \pm {v_{observer}}}}{{{v_{sound}} \pm {v_{source}}}}} \right)$ ……………..(1)
where ${v_{sound}}$ is the velocity of sound.

Complete step by step answer:
Given:
The original frequency of the sound here is ${f_i} = 640Hz$.
The velocity of the source is ${v_{source}} = \dfrac{{100}}{3}m/s$.
The velocity of sound is ${v_{sound}} = 340m/s$.
The velocity of the observer is ${v_{observer}} = 0m/s$.
To get: The observed frequency $f$.

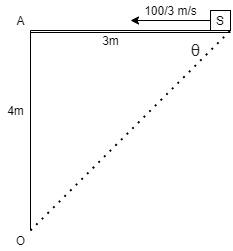
Step 1:
From the figure, you can see that $\Delta SAO$ is a right-angled triangle.
So, you can calculate
$
  O{S^2} = S{A^2} + A{O^2} \\
   = {3^2} + {4^2} \\
   = 9 + 16 \\
   = 25 \\
 $
Hence, $OS = \sqrt {25} m = 5m$.
So, you get $\cos \theta = \dfrac{3}{5}$
Step 2:
The source is not directly coming towards the observer. So, you need to resolve the component along $OS$. So, the component of the velocity of the source towards the observer is
$
  {v_s} = {v_{source}} \times \cos \theta \\
  \therefore {v_s} = \dfrac{{100}}{3} \times \dfrac{3}{5}m/s = 20m/s \\
 $
Step 3:
You can put down the values and calculate the observed frequency of the sound from eq (1)
$
  f = {f_i} \times \left( {\dfrac{{{v_{sound}}}}{{{v_{sound}} - {v_s}}}} \right) \\
   \Rightarrow f = 640 \times \left( {\dfrac{{340}}{{340 - 20}}} \right)Hz \\
   \Rightarrow f = 640 \times \left( {\dfrac{{340}}{{320}}} \right)Hz \\
  \therefore f = 2 \times 340Hz = 680Hz \\
 $

The value of the observed frequency $f$ is $680Hz$. Hence, option(B) is correct.

Note:
Here the tricky part is for you to realize that the source is advancing towards the observer with only a component directed towards it. The other one being perpendicular would have literally no effect. The velocity component ${v_s}$ is towards the observer $O$. Hence, the signature of ${v_s}$ in the Doppler Effect expression eq (1), should be negative. If it was going apart from $O$, then the signature would have been positive. So, you should be very careful as comparing the velocity of sound, the source velocity is generally lesser but a significant one to calculate the appropriate observed frequency.