Question

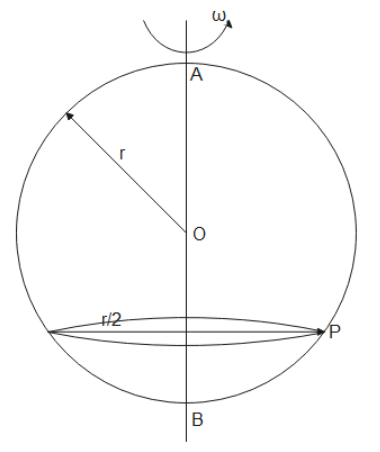
A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed ω about the vertical diameter AB, as shown in figure, the bead is at rest with respect to the circular ring at position P as shown. Then the value of ${\omega ^2}$ is equal to :

A. $\dfrac{{\left( {\dfrac{g}{{\sqrt 3 }}} \right)}}{r}$
B. $\dfrac{{\sqrt 3 g}}{{2r}}$
C. $\dfrac{{2g}}{r}$
D. $\dfrac{{2g}}{{\sqrt 3 r}}$

Answer 1

Hint: When an object is rotating in a circle its direction of velocity keeps on changing. When velocity changes there will be an acceleration and this contributes for the force. Now the force which is responsible for the change in direction in case of circular motion is called a centripetal force. We will solve the question by using this.
Formula used:
${a_c} = \dfrac{{{v^2}}}{R} = R{\omega ^2}$

Complete answer:
Centripetal force is given by the formula ${F_C} = \dfrac{{m{v^2}}}{R}$
Where ‘v’ is the magnitude of velocity of rotation and ‘R’ is the radius of the circle of the circular motion and ‘m’ is the mass of the object which is rotating in a circle.
Force will be the product of mass and acceleration. So the centripetal acceleration will be
${a_c} = \dfrac{{{v^2}}}{R}$
We know that $v = R\omega $
So the centripetal acceleration will be ${a_c} = \dfrac{{{v^2}}}{R} = R{\omega ^2}$
If we refer the diagram below we can find that

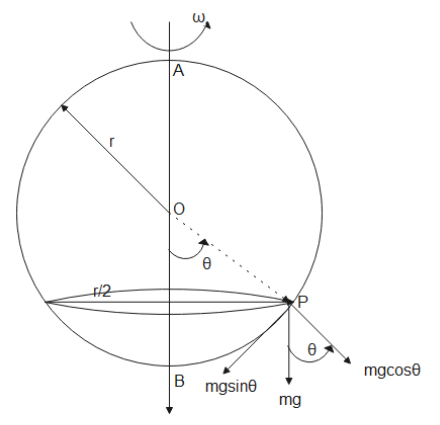
It is given that the bead is at rest. So forces will be balanced in both radial and tangential directions.
In the above diagram $mg\cos \theta $ component will be balanced by the normal reaction and component of centripetal force.
Along the tangential direction $mg\sin \theta $ component will be balanced only by $mR{\omega ^2}\cos \theta $ component.
where $R = \dfrac{r}{2}$
So by equating them we will get
$\eqalign{
  & mR{\omega ^2}\cos \theta = mg\sin \theta \cr
  & \Rightarrow \sin \theta = \dfrac{{\dfrac{r}{2}}}{r} = \dfrac{1}{2} \cr
  & \Rightarrow \theta = {30^0} \cr
  & \Rightarrow \tan \theta = \tan {30^0} = \dfrac{1}{{\sqrt 3 }} \cr
  & \Rightarrow mR{\omega ^2}\cos \theta = mg\sin \theta \cr
  & \Rightarrow {\omega ^2} = \dfrac{{g\tan \theta }}{R}{\text{ and R = }}\dfrac{r}{2} \cr
  & \Rightarrow {\omega ^2} = \dfrac{{2g\tan {{30}^0}}}{r} \cr
  & \therefore {\omega ^2} = \dfrac{{2g}}{{\sqrt 3 r}} \cr} $

Hence option D is the correct answer.

Note:
Here they had mentioned that the bead is at rest with respect to the rotating wire. This means that if we observe from a wire frame of reference the bead is stationary. The motion of wire will be the same as motion of bead i.e. circular. From the ground frame of reference the bead is rotating in a circle but from the wire frame of reference the bead is in equilibrium so we equated the forces in tangential direction.