Question

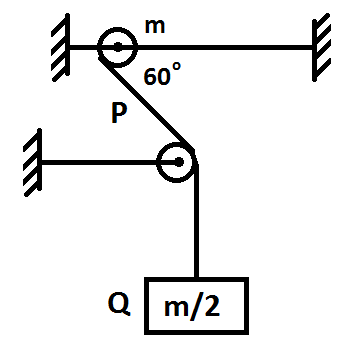
A smooth ring P of mass $m$ can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley and carries a block Q of mass $\dfrac{m}{2}$ as shown in the figure. At an instant, the string between the ring and the pulley makes an angle ${{60}^{\circ }}$ with the rod.
The initial acceleration of the ring is:

$\begin{align}
  & \text{A}\text{. }\dfrac{2g}{3} \\
 & \text{B}\text{. }\dfrac{g}{6} \\
 & \text{C}\text{. }\dfrac{2g}{9} \\
 & \text{D}\text{. }\dfrac{g}{3} \\
\end{align}$

Answer 1

Hint: To find the initial acceleration of the ring, we need to calculate the net force acting on the block, and its net acceleration in the downward direction. The constraint in the given set-up is the length of the string.

Complete answer:
Tension is a kind of force that is applied to a string. If we have an object of mass $m$ hanging on a string with a downward acceleration due to gravity, $g$, on that object, the tension on the string, is equal to the force of gravity on the object, $F=mg$.
For mass not to be in equilibrium, the net force will be equal to the acceleration of the mass $F-mg=ma$.
We are given that a smooth ring of mass $m$ can slide on a fixed horizontal rod. At an instant, the string between the ring and the pulley makes an angle ${{60}^{\circ }}$ with the rod. We need to calculate the initial acceleration of the ring.

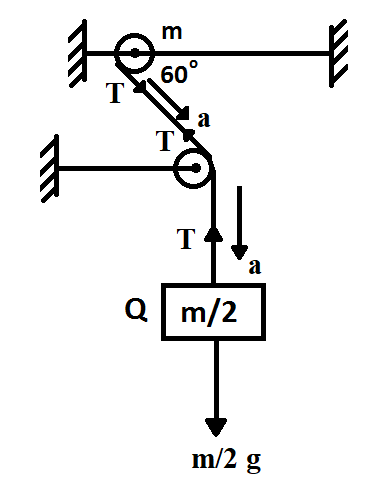
Consider $a'$ be the initial acceleration of the ring,
Applying the equation for newton’s second law on the ring
\[T\cos \left( {{60}^{\circ }} \right)=ma'=ma\cos \left( {{60}^{\circ }} \right)\]
We get,
$T=ma$
(Let’s say equation 1)
Applying the equation for newton’s second law on the block,
$\left( \dfrac{m}{2} \right)a=\dfrac{mg}{2}-T$
From equation 1, we have, $T=ma$
Therefore,
$\begin{align}
  & \left( \dfrac{m}{2} \right)a=\dfrac{mg}{2}-ma \\
 & \dfrac{3ma}{2}=\dfrac{mg}{2} \\
 & a=\dfrac{g}{3} \\
\end{align}$
Acceleration of the ring is given by,
$a'=a\cos {{60}^{\circ }}$
Put $a=\dfrac{g}{3}$
We get,
$\begin{align}
  & a'=\dfrac{g}{3}\times \dfrac{1}{2} \\
 & \left( \because \cos {{60}^{\circ }}=\dfrac{1}{2} \right) \\
 & a'=\dfrac{g}{6} \\
\end{align}$
The initial acceleration of the ring is $\dfrac{g}{6}$

Hence, the correct option is B.

Note:
For solving an interconnected motion between the ring and the mass connected with the help of pulley, we can apply the constraint equation. The constraint rule states that if we consider all the block + pulley + string as one system, then the tension becomes an internal force and we know that the work done by the internal force is zero. This implies that acceleration of the pulley or ring can have a linear relation with the acceleration of the block, according to the arrangement of the system.