Question

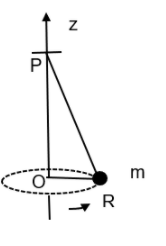
A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in a X-Y plane with centre at O and constant angular speed \[\omega \]. If the angular momentum of the system calculated about O and P are denoted by \[{{\overrightarrow{L}}_{0}}\text{ and }\overrightarrow{{{L}_{p}}},\] respectively, then:

A.\[{{\overrightarrow{L}}_{0}}\text{ and }\overrightarrow{{{L}_{p}}}\] do not vary with time.
B.\[{{\overrightarrow{L}}_{0}}\text{ }\]varies with time while \[\overrightarrow{{{L}_{p}}}\] remains constant
C.\[{{\overrightarrow{L}}_{0}}\]remains constant and \[\overrightarrow{{{L}_{p}}}\]varies with time.
D.\[{{\overrightarrow{L}}_{0}}\text{ and }\overrightarrow{{{L}_{p}}}\]both vary with time.

Answer 1

Hint: The angular momentum is a vector quantity which varies with the point under consideration. Here, the angular momentum of the same body as observed from two different points the centre of rotation O and the fixed-point P are considered.
Formula Used: The angular momentum is calculated using the formula:
 \[\begin{align}
  & \overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p} \\
 & \text{or} \\
 & \overrightarrow{L}=m(\overrightarrow{r}\times \overrightarrow{v}) \\
\end{align}\]
Where, \[\overrightarrow{L}\] is the angular momentum
 \[\overrightarrow{r}\] is the radius of the circle in which the mass undergoes circular motion
 \[\overrightarrow{p}\] is the linear momentum
  \[v\] is the linear velocity

Complete answer:
Angular momentum is the measure of linear momentum in a circular motion. It is a vector quantity like the linear momentum.
Let us consider the given situation. An object of mass m attached to a fixed string at point P is rotating around a fixed-point O with a constant angular velocity \[\omega \]. We have to determine the angular momenta experienced by the body with respect to point O and P.
 

We can begin with the point O, the center of rotation.
 \[\overrightarrow{{{L}_{0}}}=\overrightarrow{r}\times \overrightarrow{p}\]
The linear momentum ‘mv’ being substituted gives, \[\overrightarrow{{{L}_{o}}}=m(\overrightarrow{r}\times \overrightarrow{v})\]
We know that the angular velocity is a constant. Also, the radius of the rotation is a constant.
\[\begin{align}
  & \Rightarrow \overrightarrow{{{L}_{o}}}=m(\overrightarrow{OR}\times \overrightarrow{v)} \\
 & \Rightarrow \left| \overline{{{L}_{o}}} \right|=mrv \\
 & \\
\end{align}\]
The magnitude of the angular momentum at O remains constant throughout.

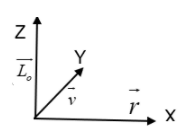
And, the direction of the angular momentum at O is always along the Z-direction.
Now, let us consider the angular momentum at point P due to the mass.
\[\begin{align}
  & \Rightarrow \overrightarrow{{{L}_{p}}}=m(\overrightarrow{PR}\times \overrightarrow{v}) \\
 & \Rightarrow \overrightarrow{{{L}_{p}}}=m((\overrightarrow{PO}+\overrightarrow{OR})\times \overrightarrow{v}) \\
\end{align}\]
It is clear from the above equation that \[\overrightarrow{PR}\]changes its direction at every instant. As a result, the direction of the angular momentum at P keeps on varying with time.
And the magnitude is given by,
 \[\begin{align}
  & \overrightarrow{{{L}_{p}}}=m\left| \overrightarrow{PR} \right|\overrightarrow{v}\widehat{k} \\
 & \left| \overrightarrow{{{L}_{p}}} \right|=m\left| \overrightarrow{PR} \right|\overrightarrow{v} \\
\end{align}\]
Which remains constant with time.
From the above, we can conclude that \[\overrightarrow{{{L}_{o}}}\]remains constant both in direction and magnitude, whereas, \[\overrightarrow{{{L}_{p}}}\]has a constant magnitude, but the direction changes.
Therefore, \[\overrightarrow{{{L}_{o}}}\] remains constant and \[\overrightarrow{{{L}_{p}}}\]varies with time.

The right answer is given by option C.

Additional Information:
We can calculate the angular momentum by using the angular velocity, \[\overrightarrow{\left| L \right|}=m{{\omega }^{2}}r\].

Note:
The angular momentum in a closed system remains constant. It is a conserved quantity. As the linear momentum is conserved as long as no external force is applied, the angular momentum is conserved as long as the torque is zero.