Question

A small magnet of moment $4.8 \times 10^{-2}\;JT^{-1}$ is suspended freely in the plane of a uniform magnetic field of magnitude $3 \times 10^{-2}\;T$. If the magnet is slightly displaced from its stable equilibrium and released then the angular frequency of its oscillations in $rad.s^{-1}$ is: (Moment of inertia of the magnet about the axis of rotation is $2.25 \times 10^{-5}\;kgm^2$)
A. 8
B. 4
C. 3
D. 2

Answer 1

Hint: Recall that when a magnet is placed in a magnetic field and is displaced from its equilibrium position it experiences a torque. We know that this torque is a result of the magnetic moment produced under the influence of the uniform magnetic field. This torque subsequently produces an angular acceleration about the moment of inertia of the magnet in a direction opposite to that of the angular displacement. Use the previous two statements to arrive at two expressions for torque.
By equating the above two equations, arrive at an expression for the ratio of the angular displacement and angular acceleration, which is what the time period of magnetic oscillation is proportional to. To this end, rearrange the time period equation to arrive at the angular frequency, following which you can substitute the values given and arrive at the appropriate result.

Formula used: Rotational torque $\tau = |m||B|sin\theta$ or $\tau= I\alpha$
Angular frequency $\omega = \sqrt{\dfrac{mB}{I}}$

Complete step by step answer:
We know that when an electric dipole is placed in a uniform electric field, it experiences a moment or torque. Similarly, whenever a magnetic dipole or a magnet is placed in a magnetic field it also experiences a torque.

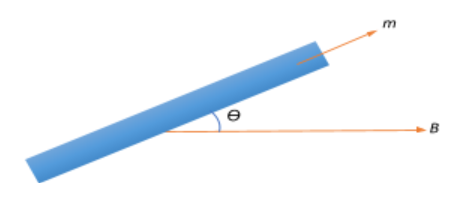
If $\vec{m}$ is the moment of the magnetic force experienced by the magnet when placed in a uniform magnetic field $\vec{B}$ while being slightly displaced by an angle $\theta$ from its equilibrium position, then the angular torque experienced by the magnet can be given as:
$\tau = \vec{m} \times \vec{B} = |m||B|sin\theta$
Given that $\theta$ is very small, then $sin\theta \approx \theta \Rightarrow \tau = |m||B|\theta$
Now, this torque produces an angular acceleration $\alpha$ about the moment of inertia I of the magnet:
$\Rightarrow \tau = I\alpha$
Equating the two torque relations we get: $|m||B|\theta = I\alpha \Rightarrow \dfrac{\theta}{\alpha} = \dfrac{I}{|m||B|}$
Now, we know that the time period of the angular simple harmonic motion is given as:
$T = 2\pi\sqrt{\dfrac{\theta}{\alpha}}$
$\Rightarrow T =2\pi\sqrt{\dfrac{I}{|m||B|}}$
$\Rightarrow \dfrac{2\pi}{T} = \sqrt{\dfrac{|m||B|}{I}} \Rightarrow \omega = \sqrt{\dfrac{|m||B|}{I}} $ , since $\omega = 2\pi f = \dfrac{2\pi}{T}$
Given that $m = 4.8 \times 10^{-2}\;JT^{-1}$, $B =3 \times 10^{-2}\;T $ and $I = 2.25 \times 10^{-5}\;kgm^2$,
$\omega = \sqrt{\dfrac{4.8 \times 10^{-2} \times 3 \times 10^{-2}}{2.25 \times 10^{-5}}} = \sqrt{\dfrac{14.4 \times 10^{-4}}{2.25 \times 10^{-5}}} = \sqrt{6.4 \times 10} = \sqrt{64} = 8\; rad.s^{-1}$

So, the correct answer is “Option A”.

Note: Remember that the two magnetic poles of a magnet placed in a uniform magnetic field experience that same magnitude of magnetic force but in opposite directions. This means that the net force acting on the magnet is zero, and there is no translatory motion of the magnet and any movement arising as a result of this force is purely rotational, which gives rise to the angular displacement that we saw in the problem.
Also, do not forget that the angular acceleration produced as a consequence of the torque acting on the magnet is always in a direction opposite to that of the angular displacement, since the oscillations are simple harmonic in nature and the restoring force, and consequently the angular acceleration is directed back towards the equilibrium position of the magnet.