Question

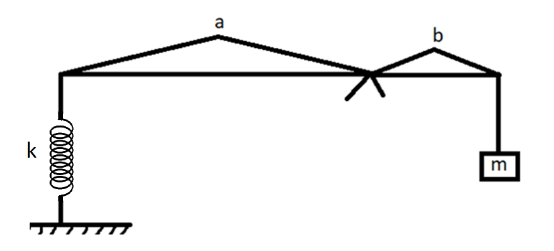
A small block of mass $ {\text{m}} $ is connected to a massless rod, which in terms attached in a spring of force constant $ k $ , as shown in fig. If the block is displaced down slightly, and left free, then the time period of oscillation is?

(A) $ 2\pi \sqrt {\dfrac{m}{k}} $
(B) $ 2\pi \left( {\dfrac{a}{b}} \right)\sqrt {\dfrac{m}{k}} $
(C) $ 2\pi \left( {\dfrac{b}{a}} \right)\sqrt {\dfrac{m}{k}} $
(D) $ 2\pi \sqrt {\dfrac{k}{m}} $

Answer 1

Hint: This could be simply solved by breaking the diagrams into simple free body diagrams of both the blocks. Then we need to apply the frequency formula.

Formula used: Here, we will use the frequency formula:
 $ {\omega _n} = \dfrac{g}{\vartriangle } $
Here, $ {\omega _n} $ is the frequency
 $ \vartriangle $ is the deflection in the spring
Also,
 $ {\omega _n} = \dfrac{{2\pi }}{T} $
Here, $ T $ is the time period.

Complete step by step solution:
We will assume $ F $ force acting at the left side on stretching of the spring due to the mass $ {\text{m}} $ .
We will start by balancing the forces to find spring force,
 $ F \times k = mg $
 $ \Rightarrow F = \dfrac{{mg}}{k} $
Let us assume the deflection in spring be $ k $
 $ x = \dfrac{b}{a} $
Deflection on mass $ {\text{m}} $ :
 $ \vartriangle {\text{ = }}\dfrac{{\text{b}}}{{\text{a}}}\left( {{\text{deflection of spring}}} \right) $
 $ \Rightarrow \vartriangle {\text{ = }}\dfrac{{\text{b}}}{{\text{a}}}\left( {\dfrac{{mg}}{k}} \right) \times \dfrac{b}{a} = \dfrac{{mg{b^2}}}{{k{a^2}}} $
Also,
 $ {\omega _n} = \dfrac{g}{\vartriangle } = \sqrt {\dfrac{{kg}}{{mg{{\left( {\dfrac{b}{a}} \right)}^2}}}} $
Equating the formula,
 $ {\omega _n} = \dfrac{{2\pi }}{T} $
 $ \Rightarrow \dfrac{{2\pi }}{T} = \sqrt {\dfrac{k}{{m{{\left( {\dfrac{b}{a}} \right)}^2}}}} $
On solving further, we get
 $ T = 2\pi \left( {\dfrac{b}{a}} \right)\sqrt {\dfrac{m}{k}} $
Then we need to match the correct option.
The correct option is C.

Additional information:
A pulley is a wheel on an axle or shaft that is designed to support movement and change of direction of a taut cable or belt, or transfer of power between the shaft and cable or belt. In the case of a pulley supported by a frame or shell that does not transfer power to a shaft, but is used to guide the cable or exert a force, the supporting shell is called a block, and the pulley may be called a sheave

Note:
It should always be kept in mind that we should always draw the FBD of the body before solving any force questions. Also, never forget to assume tension force away from the body wherever there is rope in pulley or block questions. Similarly, spring forces also are there is case of springs acting tensile (away) from the body. Also, if the bodies are connected together, they will have the same acceleration.