Question

A series LCR circuit with \[R = {\text{22 }}\Omega {\text{ }}\], \[{\text{L = }}\,\,{\text{1}}{\text{.5 H}}\]and \[C = {\text{40 \mu F}}\] is connected to a variable frequency \[V{\text{ = }}\,{\text{220 V }}\]ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
A. \[2000\,{\text{W}}\]
B. \[2200\,{\text{W}}\]
C. \[2400\,{\text{W}}\]
D. \[2500\,{\text{W}}\]

Answer 1

Hint: Use the formulae,
\[{I_{rms}} = \dfrac{{{V_{rms}}}}{Z}\] and \[P{\text{ = }}{V_{rms}} \times {I_{rms}} \times \cos \theta \].

Complete step by step solution:
An RLC circuit is an electrical circuit that consists of a resistor, inductor, and capacitor that is connected in series or parallel. When the supply frequency equals the normal circuit frequency, resonance occurs. A series RLC circuit's resonance occurs when the inductive and capacitive reactions are equal in magnitude but cancel each other out since they are \[180\] degrees apart in phase. The sharp impedance minimum that occurs is useful in tuning applications.

If \[{X_L} = {X_C}\] and the imaginary part of the transfer function is zero, resonance occurs. In resonance the circuit impedance is equal to the value of resistance as \[R = Z\].

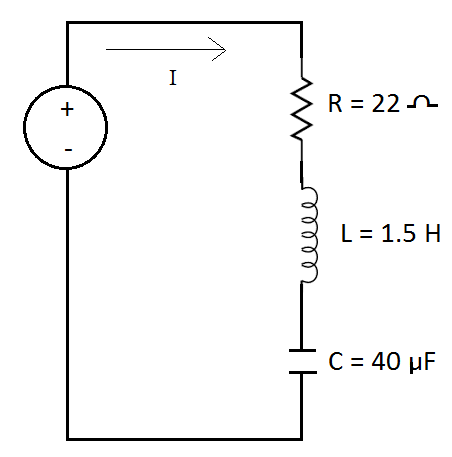
The formula of power in a LCR circuit is given by the equation:
\[P\,{\text{ = }}\,{V_{rms}} \times {I_{rms}} \times \cos \theta \] …… (1)
Where,
\[{V_{rms}}\] indicates RMS voltage.
\[{I_{rms}}\] indicates RMS current.
\[\theta \] indicates phase difference.

To find the RMS current, apply the formula:

\[{I_{rms}} = \dfrac{{{V_{rms}}}}{Z}\] …… (2)
When the supply frequency equals the normal circuit frequency, resonance occurs, then,
Impedance is equal to the resistance provided or connected in the circuit.

\[
  Z = R \\
  Z = 22\,\Omega \\
\]

When the supply frequency equals the normal circuit frequency, the RMS value of voltage is equal to the supplied voltage. So,

\[{V_{rms}}{\text{ = }}\,\,V = \,\,{\text{220 V}}\]

Substitute the values \[{V_{rms}}{\text{ = 220 V}}\]and \[Z = 22\,\Omega \] in equation (2):

 \[
  {I_{rms}} = \dfrac{{{V_{rms}}}}{Z} \\
   = \dfrac{{220}}{{22}} \\
   = 10\,{\text{A}} \\
\]
Now, substitute the values \[{V_{rms}}{\text{ = 220 V}}\], \[{I_{rms}} = 10\,{\text{A}}\]and \[\theta = 0^\circ \](in case of resonance circuit phase angle is always zero degree) in equation (1):

\[
  P\,{\text{ = }}\,{V_{rms}} \times {I_{rms}} \times \cos \theta \\
   = 220\,{\text{V}} \times 10\,{\text{A}} \times \cos 0^\circ \\
   = 220 \times 10 \times 1\,{\text{W}} \\
  {\text{ = 2200}}\,{\text{W}} \\
\]
Hence, the power transferred to the circuit in one complete cycle is \[{\text{2200}}\,{\text{W}}\].

Note: In this problem we are asked to find the average power transferred to the circuit in one complete cycle. For this, we need to apply the formula to find the RMS current. While doing so, in a resonant circuit impedance is equal to the resistance provided or connected in the circuit. It is important to note that the trigonometric ratio in the power formula is always cosine not sine and the phase angle is always zero degree.