Answer
377.1k+ views
Hint: In this problem we have to find the total cost of painting the roller pin made of \[3\] cylinders. We need to find the total surface area of the roller pin. We will find the surface area of each roller and then add them to find the total area. We will also have to subtract the area of \[2\] circular base of small cylinder plates.
We use the formula for finding the total surface area of cylinder \[ = \] \[2\pi r(h + r)\]
Complete step by step solution:
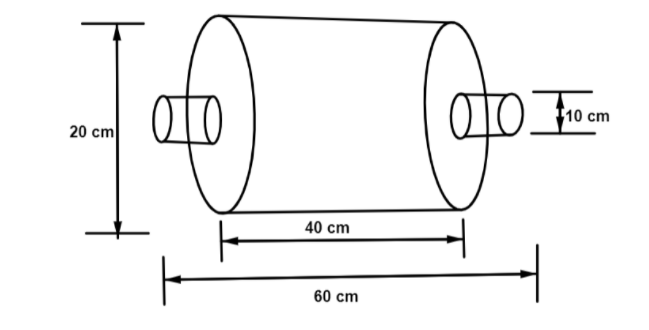
We are given the diagram which represent a roller pin is made up of \[3\] cylindrical plates made of wood is given below,
This problem is based on the area of \[3\] -Dimensional solid figures. The Cylinder is a \[3\] -D solid figure which has two parallel circular bases joined by a curved surface. Volume of the cylinder is given by \[\pi {r^2}h\] where \[r\] is the radius of the base and \[h\] is the height of the cylinder.
Area of the circular base is given by \[\pi {r^2}\] where r is the radius of the base.
Consider the given question,
Height of larger cylinder \[ = \] \[40\] \[cm\]
Hence radius of larger cylinder \[ = \] \[\dfrac{{20}}{2} = 10\] \[cm\]
Total surface area of larger cylinder
\[ = \] \[2\pi r(h + r) = 2 \times \dfrac{{22}}{7} \times 10 \times (40 + 10)\] \[c{m^2}\]
Hence, the total surface area of larger cylinder
\[ = \] \[\dfrac{{22000}}{7}\] \[c{m^2}\]
Now the length of \[2\] smaller cylinder
\[ = \] \[60 - 40 = 20\] \[cm\]
Therefore, length of each smaller cylinder \[ = \] \[10\] \[cm\]
We have to calculate the total surface area of smaller cylinder and area of roller pin, then
Radius of each smaller cylinder
\[ = \] \[\dfrac{{10}}{2} = 5\] \[cm\]
Area of circular base
\[ = \] \[\pi {r^2} = \dfrac{{22}}{7} \times 5 \times 5 = \dfrac{{550}}{7}\] \[c{m^2}\]
Total surface area of smaller cylinder
\[ = \] \[2\pi r(h + r) = 2 \times \dfrac{{22}}{7} \times 5 \times (10 + 5) = \dfrac{{3300}}{7}\] \[c{m^2}\]
Total surface area of roller pin
\[ = \] (TSA of larger cylinder \[ + \] \[2\] \[ \times \] TSA of smaller cylinder \[ - \] \[2\] \[ \times \] area of circular base)
Total surface area of roller pin
\[ = \] \[\left( {\dfrac{{22000}}{7} + 2 \times \dfrac{{3300}}{7} - 2 \times \dfrac{{550}}{7}} \right) = \dfrac{{27500}}{7}\] \[c{m^2}\]
Hence, The total surface area of roller pin
\[ = \] \[\dfrac{{27500}}{7}\] \[c{m^2}\]
Now cost of painting \[ = \] \[14\] paisa per \[c{m^2}\]
Total cost of painting roller pin \[ = \] \[\dfrac{{27500}}{7} \times 14 = 55,000\]
Hence, Total cost of painting roller pin is Rs. \[55,000\] Paisa.
which will be equal to Rs 550.
So, the correct answer is “ Rs. Rs 550. ”.
Note: We note that the formulas are used in this given problem,
Radius is half the length of diameter.
Total surface area of roller pin \[ = \] (TSA of larger cylinder \[ + \] \[2\] \[ \times \] TSA of smaller cylinder \[ - \] \[2\] \[ \times \] area of circular base)
Volume of cylinder \[ = \] \[\pi {r^2}h\]
Curved surface area of cylinder \[ = \] \[2\pi rh\] .
We use the formula for finding the total surface area of cylinder \[ = \] \[2\pi r(h + r)\]
Complete step by step solution:
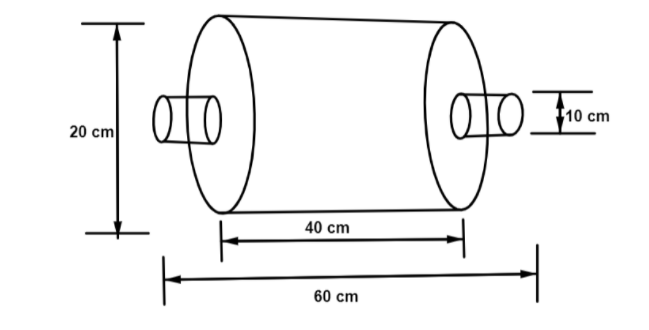
We are given the diagram which represent a roller pin is made up of \[3\] cylindrical plates made of wood is given below,

This problem is based on the area of \[3\] -Dimensional solid figures. The Cylinder is a \[3\] -D solid figure which has two parallel circular bases joined by a curved surface. Volume of the cylinder is given by \[\pi {r^2}h\] where \[r\] is the radius of the base and \[h\] is the height of the cylinder.
Area of the circular base is given by \[\pi {r^2}\] where r is the radius of the base.
Consider the given question,
Height of larger cylinder \[ = \] \[40\] \[cm\]
Hence radius of larger cylinder \[ = \] \[\dfrac{{20}}{2} = 10\] \[cm\]
Total surface area of larger cylinder
\[ = \] \[2\pi r(h + r) = 2 \times \dfrac{{22}}{7} \times 10 \times (40 + 10)\] \[c{m^2}\]
Hence, the total surface area of larger cylinder
\[ = \] \[\dfrac{{22000}}{7}\] \[c{m^2}\]
Now the length of \[2\] smaller cylinder
\[ = \] \[60 - 40 = 20\] \[cm\]
Therefore, length of each smaller cylinder \[ = \] \[10\] \[cm\]
We have to calculate the total surface area of smaller cylinder and area of roller pin, then
Radius of each smaller cylinder
\[ = \] \[\dfrac{{10}}{2} = 5\] \[cm\]
Area of circular base
\[ = \] \[\pi {r^2} = \dfrac{{22}}{7} \times 5 \times 5 = \dfrac{{550}}{7}\] \[c{m^2}\]
Total surface area of smaller cylinder
\[ = \] \[2\pi r(h + r) = 2 \times \dfrac{{22}}{7} \times 5 \times (10 + 5) = \dfrac{{3300}}{7}\] \[c{m^2}\]
Total surface area of roller pin
\[ = \] (TSA of larger cylinder \[ + \] \[2\] \[ \times \] TSA of smaller cylinder \[ - \] \[2\] \[ \times \] area of circular base)
Total surface area of roller pin
\[ = \] \[\left( {\dfrac{{22000}}{7} + 2 \times \dfrac{{3300}}{7} - 2 \times \dfrac{{550}}{7}} \right) = \dfrac{{27500}}{7}\] \[c{m^2}\]
Hence, The total surface area of roller pin
\[ = \] \[\dfrac{{27500}}{7}\] \[c{m^2}\]
Now cost of painting \[ = \] \[14\] paisa per \[c{m^2}\]
Total cost of painting roller pin \[ = \] \[\dfrac{{27500}}{7} \times 14 = 55,000\]
Hence, Total cost of painting roller pin is Rs. \[55,000\] Paisa.
which will be equal to Rs 550.
So, the correct answer is “ Rs. Rs 550. ”.
Note: We note that the formulas are used in this given problem,
Radius is half the length of diameter.
Total surface area of roller pin \[ = \] (TSA of larger cylinder \[ + \] \[2\] \[ \times \] TSA of smaller cylinder \[ - \] \[2\] \[ \times \] area of circular base)
Volume of cylinder \[ = \] \[\pi {r^2}h\]
Curved surface area of cylinder \[ = \] \[2\pi rh\] .
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE

Mark and label the given geoinformation on the outline class 11 social science CBSE

When people say No pun intended what does that mea class 8 english CBSE

Name the states which share their boundary with Indias class 9 social science CBSE

Give an account of the Northern Plains of India class 9 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

Give 10 examples for herbs , shrubs , climbers , creepers

Difference Between Plant Cell and Animal Cell

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Change the following sentences into negative and interrogative class 10 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE