Question

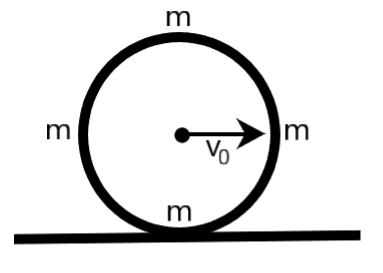
A ring of mass $m$ and radius $R$ has four particles each of mass $m$ attached to the ring as shown in the figure. The center of the ring has a speed of ${{v}_{0}}$. The kinetic energy of the system is

$\begin{align}
  & A)m{{v}_{0}}^{2} \\
 & B)3m{{v}_{0}}^{2} \\
 & C)5m{{v}_{0}}^{2} \\
 & D)6m{{v}_{0}}^{2} \\
\end{align}$

Answer 1

Hint: Each particle on the ring has rotational energy as well as translational energy. Rotational energy refers to the kinetic energy of the ring due to rotational motion whereas translational energy refers to the kinetic energy of the ring due to translational motion. The net velocity of each particle is determined. These net velocities are used to determine rotational energy, translational energy, and thus kinetic energy of each particle. The sum of kinetic energies of each particle along with that of the ring itself is equal to the total kinetic energy of the system.
Formula used:
$\begin{align}
  & 1){{E}_{T}}=\dfrac{1}{2}m{{v}^{2}} \\
 & 2){{E}_{R}}=\dfrac{1}{2}I{{\omega }^{2}}=\dfrac{1}{2}(m{{r}^{2}})\left( \dfrac{{{v}^{2}}}{{{r}^{2}}} \right)=\dfrac{1}{2}m{{v}^{2}} \\
\end{align}$
$3)E={{E}_{R}}+{{E}_{T}}$
$3){{v}_{net}}=\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}$

Complete step-by-step solution
When a ring is allowed to roll on the floor with a particular velocity, the ring is said to have both rotational energy as well as translational energy. Rotational energy refers to the kinetic energy of the ring due to rotational motion whereas translational energy refers to the kinetic energy of the ring due to translational motion. Mathematically, rotational energy and translational energy are given by
$\begin{align}
  & {{E}_{T}}=\dfrac{1}{2}m{{v}^{2}} \\
 & {{E}_{R}}=\dfrac{1}{2}I{{\omega }^{2}}=\dfrac{1}{2}(m{{r}^{2}})\left( \dfrac{{{v}^{2}}}{{{r}^{2}}} \right)=\dfrac{1}{2}m{{v}^{2}} \\
\end{align}$
where
${{E}_{T}}$ is the translational energy of a rolling ring
$m$ is the mass of the ring
$v$ is the velocity of the ring
${{E}_{R}}$ is the rotational energy of the rolling ring
$I=m{{r}^{2}}$ is the moment of inertia of the rolling ring of radius $r$
$\omega =\dfrac{v}{r}$ is the angular velocity of the rolling ring
Let this set of equations be denoted by X.
Clearly, from the set of equations denoted by X, we can understand that both translational energy and rotational energy of a rolling ring have similar formulas.
Coming to our question, we are provided with a ring of mass $m$ and radius $R$, which has four particles, each of mass $m$ attached to the ring as shown in the following figure. It is also given that the center of the ring has a speed of ${{v}_{0}}$, and the ring is moving eastwards. We are required to determine the kinetic energy of the system.
The total kinetic energy of the system is equal to the sum of total kinetic energies of each particle attached to the ring as well as the total kinetic energy of the ring itself. Firstly, let us name the points at which each particle of mass $m$ is kept on the ring, as shown in the figure. From the figure, it is also noted that the center of the ring is denoted by a point $O$, as shown.

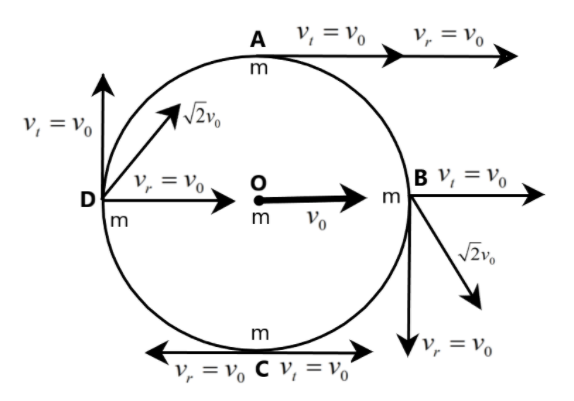
Now, let us move on to determine the net velocities of each particle of mass $m$, kept at $A, B, C$, and $D$, respectively.
Clearly, the net velocity of particle kept at $A$ is given by
${{v}_{1}}={{v}_{r}}+{{v}_{t}}={{v}_{0}}+{{v}_{0}}=2{{v}_{0}}$
where
${{v}_{1}}$ is the net velocity of particle kept at $A$ acting eastwards as shown in the diagram
${{v}_{t}}={{v}_{0}}$ is the velocity of the particle due to translational motion, acting eastwards as shown
${{v}_{r}}={{v}_{0}}$ is the velocity of the particle due to rotational motion, acting eastwards as shown
${{v}_{0}}$ is the velocity with which the ring is moving eastwards
Let this be equation 1.
Similarly, the net velocity of particle kept at $B$ is given by
${{v}_{2}}={{v}_{r}}+{{v}_{t}}=\sqrt{{{v}_{0}}^{2}+{{v}_{0}}^{2}}=\sqrt{2}{{v}_{0}}$
where
${{v}_{2}}$ is the net velocity of particle kept at $B$ acting south-eastwards, as shown in the diagram
${{v}_{t}}={{v}_{0}}$ is the velocity of the particle due to translational motion, acting eastwards, as shown
${{v}_{r}}={{v}_{0}}$ is the velocity of the particle due to rotational motion, acting downwards, as shown
$\sqrt{{{v}_{0}}^{2}+{{v}_{0}}^{2}}$ is the resultant vector of ${{v}_{t}}$ and ${{v}_{r}}$, acting south-eastwards, as shown
${{v}_{0}}$ is the velocity with which the ring is moving eastwards
Let this be equation 2.
Now, the net velocity of particle kept at $C$ is given by
${{v}_{3}}={{v}_{r}}+{{v}_{t}}=-{{v}_{0}}+{{v}_{0}}=0$
where
${{v}_{3}}=0$ is the net velocity of particle kept at $C$
${{v}_{t}}={{v}_{0}}$ is the velocity of the particle due to translational motion, acting eastwards, as shown
${{v}_{r}}={{v}_{0}}$ is the velocity of the particle due to rotational motion, acting westwards, as shown
${{v}_{0}}$ is the velocity with which the ring is moving eastwards
Let this be equation 3.
Also, the net velocity of particle kept at $D$ is given by
${{v}_{4}}={{v}_{r}}+{{v}_{t}}=\sqrt{{{v}_{0}}^{2}+{{v}_{0}}^{2}}=\sqrt{2}{{v}_{0}}$
where
${{v}_{4}}$ is the net velocity of particle kept at $D$ acting north-eastwards, as shown in the diagram
${{v}_{t}}={{v}_{0}}$ is the velocity of the particle due to translational motion, acting eastwards, as shown
${{v}_{r}}={{v}_{0}}$ is the velocity of the particle due to rotational motion, acting upwards, as shown
$\sqrt{{{v}_{0}}^{2}+{{v}_{0}}^{2}}$ is the resultant vector of ${{v}_{t}}$ and ${{v}_{r}}$, acting north-eastwards, as shown
${{v}_{0}}$ is the velocity with which the ring is moving eastwards
Let this be equation 4.
Now, if $E$ denotes the total kinetic energy of the system, then, $E$ is given by
\[E={{E}_{1}}+{{E}_{2}}+{{E}_{3}}+{{E}_{4}}+{{E}_{Ring}}=\dfrac{1}{2}m{{v}_{1}}^{2}+\dfrac{1}{2}m{{v}_{2}}^{2}+\dfrac{1}{2}m{{v}_{3}}^{2}+\dfrac{1}{2}m{{v}_{4}}^{2}+m{{v}_{0}}^{2}=\dfrac{1}{2}m\left( {{v}_{1}}^{2}+{{v}_{2}}^{2}+{{v}_{3}}^{2}+{{v}_{4}}^{2} \right)+m{{v}_{0}}^{2}\]
where
$E$ is the total kinetic energy of the system
${{E}_{1}}=\dfrac{1}{2}m{{v}_{1}}^{2}$ is the kinetic energy of particle of mass $m$ kept at $A$
${{E}_{2}}=\dfrac{1}{2}m{{v}_{2}}^{2}$ is the kinetic energy of particle of mass $m$ kept at $B$
${{E}_{3}}=\dfrac{1}{2}m{{v}_{3}}^{2}$ is the kinetic energy of particle of mass $m$ kept at $C$
${{E}_{4}}=\dfrac{1}{2}m{{v}_{4}}^{2}$ is the kinetic energy of particle of mass $m$ kept at $D$
${{E}_{Ring}}={{E}_{T}}+{{E}_{R}}=\dfrac{1}{2}m{{v}_{0}}^{2}+\dfrac{1}{2}m{{v}_{0}}^{2}=m{{v}_{0}}^{2}$ is the kinetic energy of the ring itself, from the set of equations denoted by X
Let this be equation 5.
Substituting the values of ${{v}_{1}},{{v}_{2}},{{v}_{3}}$ and ${{v}_{4}}$ from equation $1,2,3$ and $4$,respectively, in equation 5, we have
\[E=\dfrac{1}{2}m\left( {{v}_{1}}^{2}+{{v}_{2}}^{2}+{{v}_{3}}^{2}+{{v}_{4}}^{2} \right)+m{{v}_{0}}^{2}=\dfrac{1}{2}m\left( {{\left( 2{{v}_{0}} \right)}^{2}}+{{\left( \sqrt{2}{{v}_{0}} \right)}^{2}}+{{0}^{2}}+{{\left( \sqrt{2}{{v}_{0}} \right)}^{2}} \right)+m{{v}_{0}}^{2}=\dfrac{8m{{v}_{0}}^{2}}{2}+m{{v}_{0}}^{2}=5m{{v}_{0}}^{2}\]
Let this be equation 6.
Therefore, from equation 6, we come to the conclusion that the total kinetic energy of the given system is equal to $5m{{v}_{0}}^{2}$.
Hence, the correct answer is option $C$.

Note:
1). Students need not get confused with equation 3. Here, the net velocity of the particle kept at $C$ is equal to zero because both the translational motion of the particle and the rotational motion of the particle are acting in opposite directions.
2). Kinetic energy at the center of the ring is equal to the kinetic energy of the ring, itself. Students should not miss including this value of kinetic energy while determining the total kinetic energy of the system.