Question

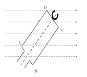
A rectangular coil ABCD is rotated anticlockwise with a uniform angular velocity about the axis shown in the Fig. The axis of rotation of the coil as well as the magnetic field B are horizontal. The induced EMF in the coil would be maximum when:
(A) The plane of the coil makes an angle of 30° with the magnetic field
(B) The plane of the coil is at right angles to the magnetic field
(C) The plane of the coil makes an angle of 45° with the magnetic field
(D) The plane of the coil is horizontal

Answer 1

Hint
When a rectangular coil is placed in a uniform magnetic field and rotated at a constant angular velocity, an EMF is induced in the coil due to the change in magnetic flux through the coil. The flux is due to the variations in the magnetic field. By using the formula to calculate the induced EMF, we can determine the position in which the EMF will be maximum.

Complete step by step answer
Let us consider the magnetic field strength be B, the area of the coil be A, and the angle between the magnetic field and the line perpendicular to the surface of the rectangular coil be θ.
The magnetic flux through the coil due to the variation in the magnetic field is φ. Then,
$\Rightarrow \varphi = \bar B.\bar A$
which gives the formula for calculating the flux through the coil.
$\Rightarrow \varphi = BA\cos \theta $
Now, the induced EMF is the change in the flux through the coil. Then,
$\Rightarrow \varepsilon = \dfrac{{d\varphi }}{{dt}}$
When we substitute the value of flux in the formula, we get,
$\varepsilon = \dfrac{{d(BA\cos \theta )}}{{dt}}$
$\Rightarrow \varepsilon = \dfrac{{BA\sin \theta d\theta }}{{dt}}$
We know that , $\theta = \omega t$
Then,
$\Rightarrow \varepsilon = BA\omega \sin \theta $
Now, we know that, the highest value of sin is 1 with $\theta = 90^\circ $
Then, as the angle between the magnetic field and the line perpendicular to the surface of the coil is 90°, the angle between the magnetic field and the plane of the coil becomes 180°.
Thus, the plane of the coil is horizontal.
Hence, the correct answer is option (D).

Note
When we consider a coil rotating with uniform angular velocity, we should know that the coil has an induced EMF due to the change in flux of the coil. The change in flux is associated with the variations in the magnetic field strength.