Question

A printed page is pressed by a glass of water. The refractive index of the glass and water is 1.5 and 1.33, respectively, if the thickness of the bottom of glass is 1 cm and depth of water is 5 cm how much the page will appear to be shifted if viewed from the top?

Answer 1

Hint: In this question we will use the relation between the apparent depth and refractive index of the medium. Further, we will use this value to find the shift. We will also discuss the basics of apparent depth and real depth for better understanding.
Formula used:
$h' = \dfrac{{{h_1}}}{{\mu {}_1}} + \dfrac{{{h_2}}}{{{\mu _2}}}$
$\Delta h = h - h'$

Complete answer:
As we know that the apparent depth in a medium is defined as the depth of an object in a denser medium when seen from the rarer medium. The value of apparent depth is smaller than the real depth.
As we know, the apparent depth is given by:
$h' = \dfrac{{{h_1}}}{{\mu {}_1}} + \dfrac{{{h_2}}}{{{\mu _2}}}$
$ \Rightarrow h' = \dfrac{1}{{1.5}} + \dfrac{5}{{1.33}} = 4.43cm$
From the above equation we can calculate normal shift as:
$\Delta h = h - h'$
$\eqalign{& \Rightarrow \Delta h = 6 - 4.43 \cr
  & \therefore \Delta h = 1.57cm \cr} $
Therefore, from the above result we can say that the page will appear to be shifted 1.57cm if viewed from the top.

Additional information:
We know that the real depth is defined as the actual distance of an object under the surface, when it is measured by submerging a perfect ruler along with it.
Apparent depth occurs due to the property of light called refraction of light.
In the diagram below, apparent depth can be observed.

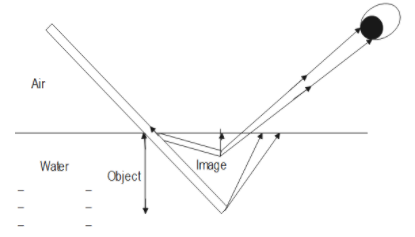
If we take an example where, when we immerse a stick in water, the rays of light pass through the rarer medium to the denser medium and this ray of light bends towards the normal. So the part of the stick that is immersed in the water appears to be broken towards the normal drawn at the interface and it gives an apparent bending. Also, the ruler appears shorter like being raised up in the water.

Note:
We should remember that the apparent depth of an object is seen due to bending of light rays towards normal, not because of actual small size. Also, we should remember that the refractive index of water is taken to be 1.