
A population of organisms has a gene for which there are two alleles, D and d. The allele frequency of D = 0.8. If this population satisfies all five of the Hardy-Weinberg conditions, what are the genotype frequencies that are expected in the next generation?
A. DD = 0.04; Dd = 0.32; dd = 0.64
B. DD = 0.64; Dd = 0.32; dd = 0.64
C. DD = 0.04; Dd= 0.64; dd= 0.32
D. DD = 0.64; Dd = 0.32; dd = 0.04
Answer
355.2k+ views
Hint: The Hardy-Weinberg model explains how a population can remain at genetic equilibrium, known as Hardy-Weinberg equilibrium. Genetic equilibrium takes place when there is no evolution within the population. In other words, the frequency of alleles (variants of a gene) will be similar from one generation to another.
Complete Step-by-step answer:
The Hardy–Weinberg principle relates allele frequencies to genotype frequencies in a randomly reproducing population. Consider a population with two alleles (A and B) that segregate at one locus. The frequency of allele A signified by p and the frequency of allele B is signified by q. The Hardy–Weinberg principle declares that after one generation of random breeding genotype frequencies will be
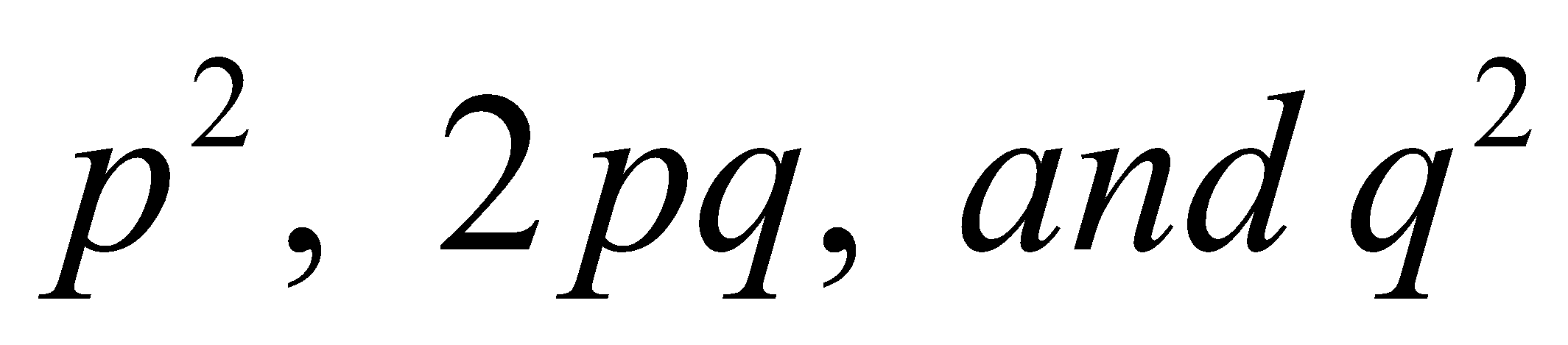 .
.
In the absence of other evolutionary forces (like natural selection), genotype frequencies should remain constant, and the population is said to be at Hardy–Weinberg equilibrium.
We are told that the allele frequency for D = 0.8; thus, the frequency of d= 0.2. These values are the p and q that we have to calculate the genotype frequencies in the next generation. By using a Hardy- Weinberg equation,
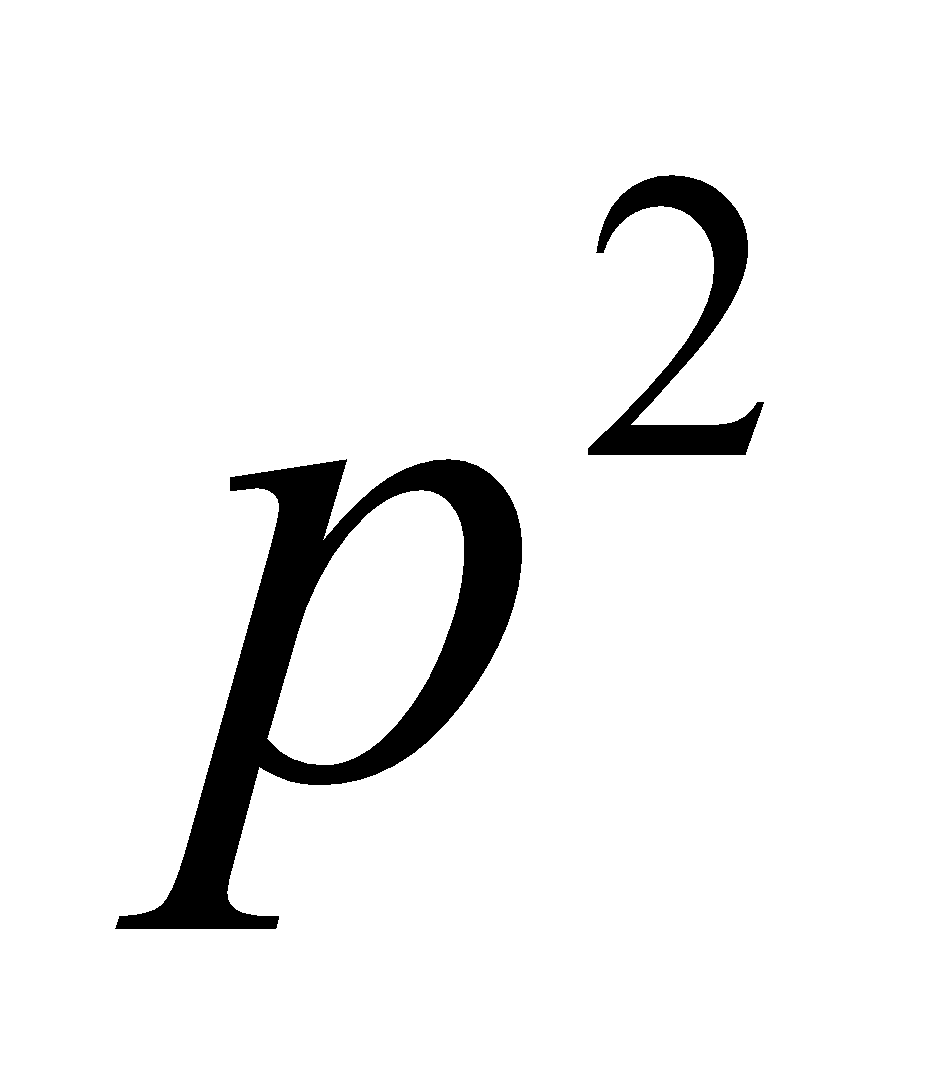 |(DD) = 0.64,
|(DD) = 0.64,
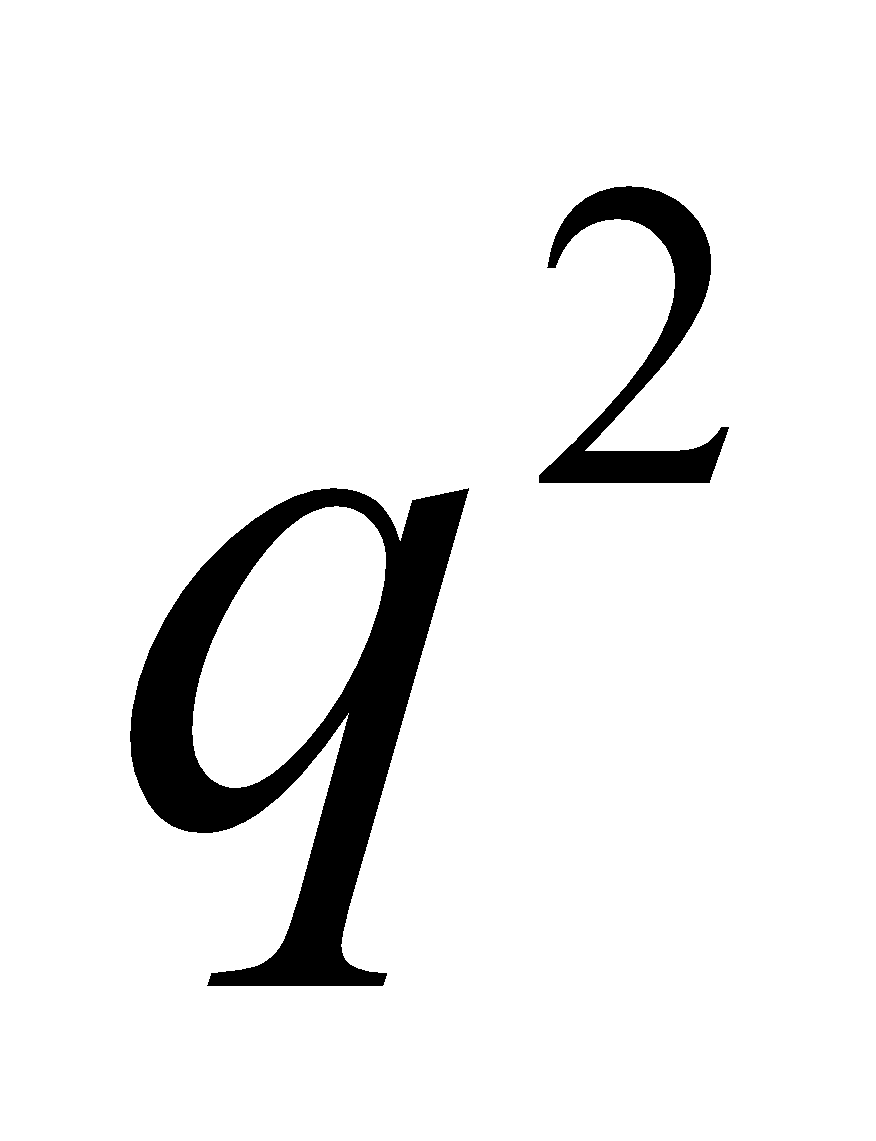 |(dd) = 0.04 and 2pq (Dd) = 0.32.
|(dd) = 0.04 and 2pq (Dd) = 0.32.
Therefore the correct answer is Option D.
Note: The Hardy–Weinberg principle is based on a number of assumptions like random mating (i.e, population structure is not present and mating takes place in direct proportion to genotype frequencies), the lack of natural selection, very high population size (i.e., genetic drift is negligible), no gene flow or migration, no mutation, and the locus is autosomal.
Complete Step-by-step answer:
The Hardy–Weinberg principle relates allele frequencies to genotype frequencies in a randomly reproducing population. Consider a population with two alleles (A and B) that segregate at one locus. The frequency of allele A signified by p and the frequency of allele B is signified by q. The Hardy–Weinberg principle declares that after one generation of random breeding genotype frequencies will be
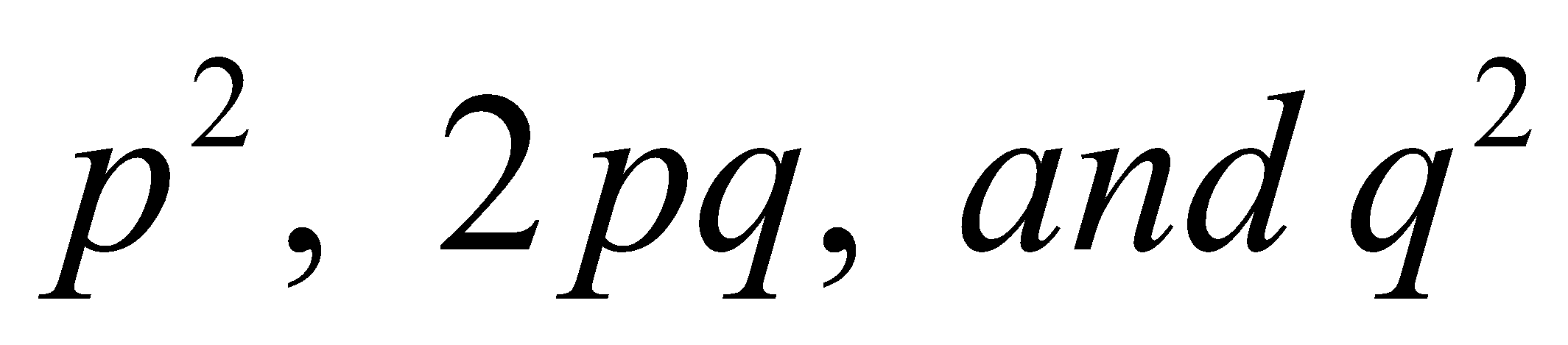
In the absence of other evolutionary forces (like natural selection), genotype frequencies should remain constant, and the population is said to be at Hardy–Weinberg equilibrium.
We are told that the allele frequency for D = 0.8; thus, the frequency of d= 0.2. These values are the p and q that we have to calculate the genotype frequencies in the next generation. By using a Hardy- Weinberg equation,
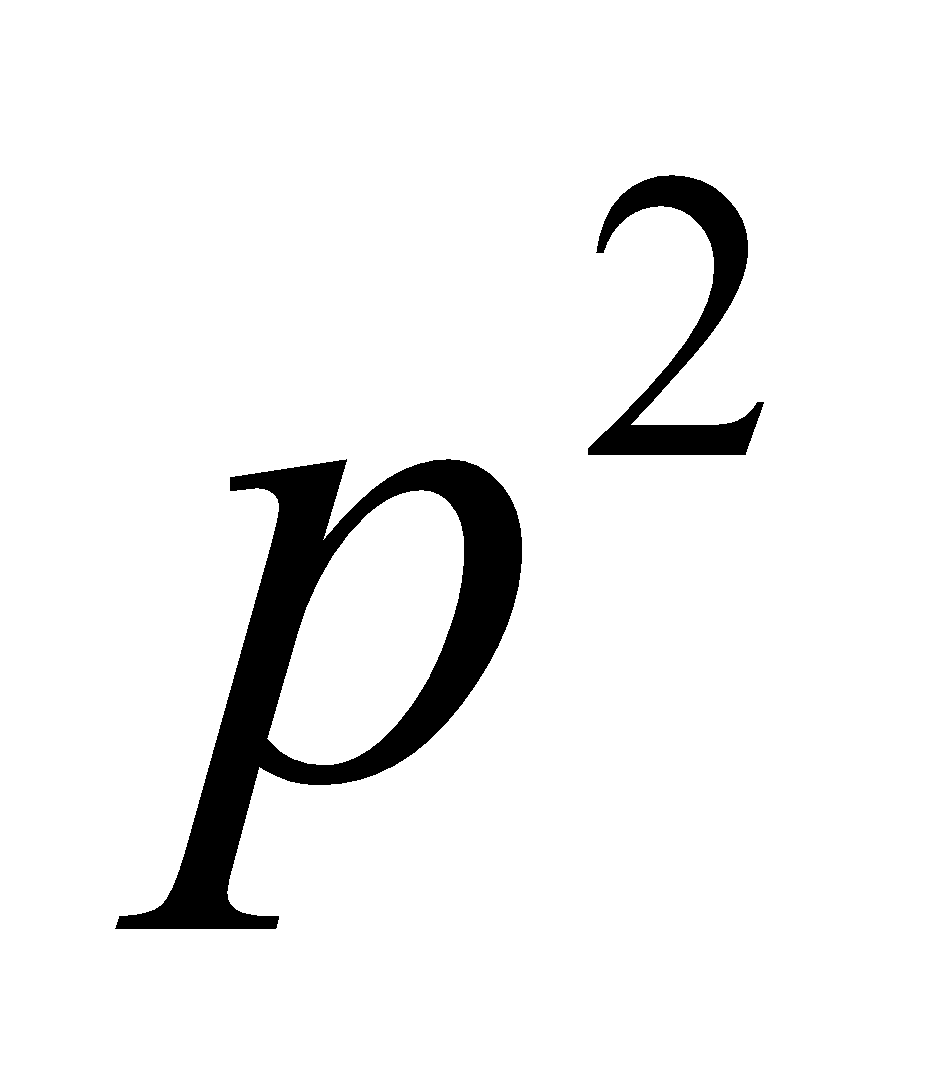
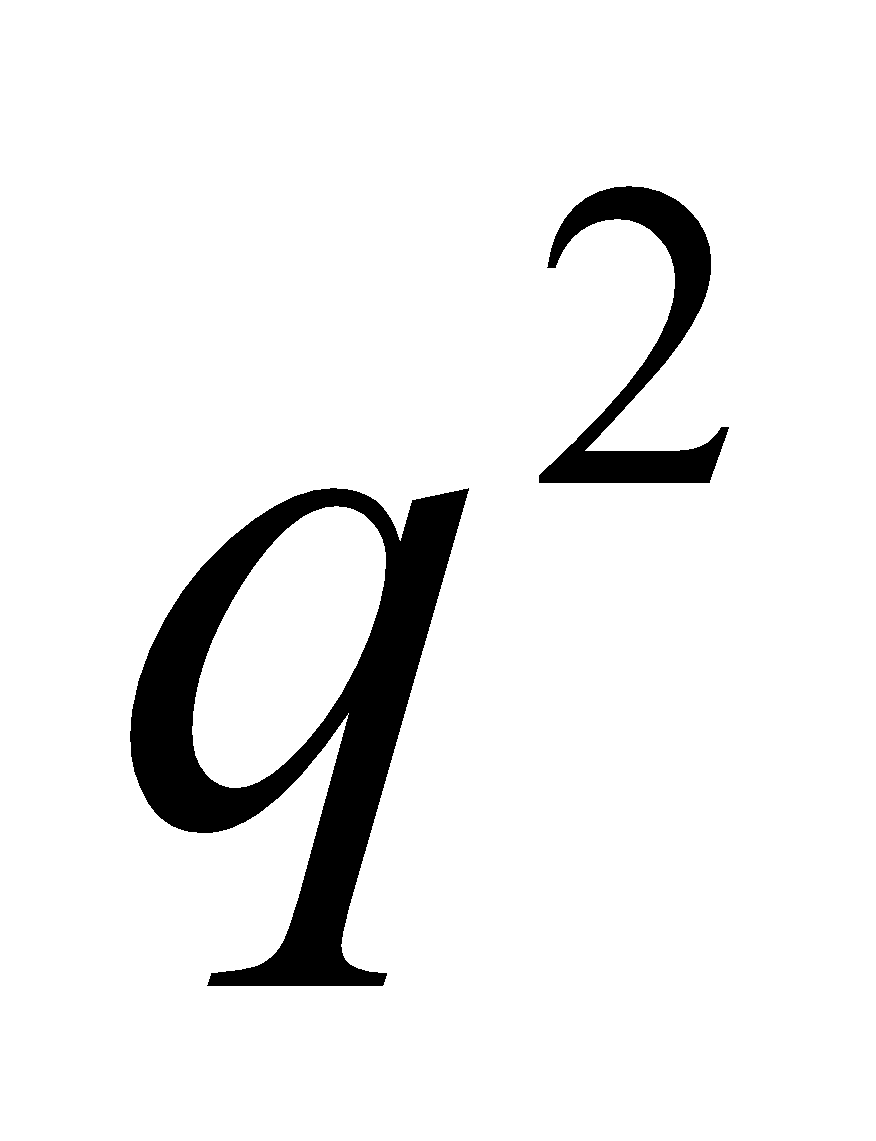
Therefore the correct answer is Option D.
Note: The Hardy–Weinberg principle is based on a number of assumptions like random mating (i.e, population structure is not present and mating takes place in direct proportion to genotype frequencies), the lack of natural selection, very high population size (i.e., genetic drift is negligible), no gene flow or migration, no mutation, and the locus is autosomal.
Recently Updated Pages
Given diagram showing a typical agarose gel electrophoresis class 13 biology NEET_UG

Capping is a process in which A adenylate is added class 12 biology NEET_UG

Explain in brief the separation and isolation of DNA class 12 biology NEET_UG

Number of testicular lobules in testes is A 250 B 500 class 12 biology NEET_UG

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

The shortest day of the year in India

What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?




