Question

A polarizer set is adjusted such that the intensity of light coming out of the analyser is just 10% of the original intensity. Assuming that the polarizer-analyser set does not absorb any light, the angle by which the analyser need to be rotated further to reduce the output intensity to be zero, is:
$\left( A \right)90^\circ $
$
  \left( B \right)71.6^\circ \\
  \left( C \right)18.4^\circ \\
  \left( D \right)45^\circ \\
 $

Answer 1

- Hint –We will start this by understanding the question properly and then we will make a diagram to understand it better. After that we will state the Law of Malus and by using the mathematical equation of the Law of Malus, i.e., $I = {I_0}{\cos ^2}\theta $, we will get the required answer.

Complete step-by-step solution -

We have to find the angle of further rotation for the analyser.
Let this angle be $\theta '$
First we will make a diagram which is as follows:

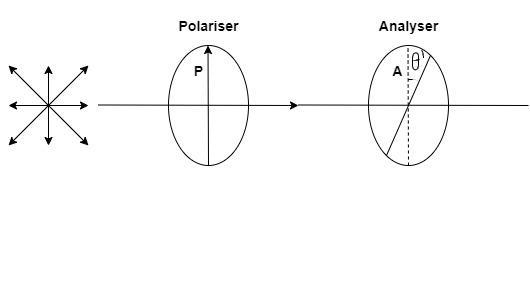
Now, we will use the mathematical equation of the Law of Malus.
We know that the law of Malus is the phenomenon in which a beam of completely plane polarized light is passed through analyser, the intensity $'I'$of a transmitted light varies directly as the square of the cosine of the angle $'\theta '$ between the transmission directions of polarizer and analyzer.” Mathematically,
$I \propto {\cos ^2}\theta $
or $I = {I_0}{\cos ^2}\theta $
Here ${I_0}$ is the maximum intensity of transmitted light.

Now, according to the given condition,
$
  I = 10\% {I_0} \\
   \Rightarrow I = \dfrac{{10}}{{100}}{I_0} \\
   \Rightarrow I = \dfrac{1}{{10}}{I_0} \\
   \Rightarrow I = \dfrac{{{I_0}}}{{10}} \\
 $

We know that from Law of Malus,
$I = {I_0}{\cos ^2}\theta $ ……….. (1)
where $\theta $is the angle between axis of polarizer and analyser.
Putting $I = \dfrac{{{I_0}}}{{10}}$ in equation (1), we obtain,
$
  \dfrac{{{I_0}}}{{10}} = {I_0}{\cos ^2}\theta \\
   \Rightarrow \dfrac{1}{{10}} = {\cos ^2}\theta \\
   \Rightarrow \cos \theta = \sqrt {\dfrac{1}{{10}}} \\
   \Rightarrow \cos \theta = \dfrac{1}{{\sqrt {10} }} \\
   \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt {10} }}} \right) \\
   \Rightarrow \theta = 71.6^\circ \\
 $

Now, if we put $\theta = 90^\circ $in equation (1) then the intensity becomes, $I = 0$ as $\cos 90^\circ = 0$.

Therefore, the angle of rotation $\left( {\theta '} \right)$ $ = \left( {90^\circ - 71.6^\circ } \right)$
$ \Rightarrow \theta ' = 18.4^\circ $
Hence, the angle by which the analyser needs to be rotated further to reduce the output intensity to be zero is $18.4^\circ $.
Therefore, option C is the right answer.

Note – A polariser is a filter that only allows specific light waves or vibrations to pass through it and focus them in a single plane. An analyser, mainly used as a second polariser, determines the quantity and the direction of the light. Due to the use of these filters, the polarised light waves vibrate in one single direction, instead of the normal one that vibrates in random directions.