Question

A point ‘ \[O\] ’ marked on the surface of a glass sphere of diameter \[20\,{\text{cm}}\] is viewed through glass from the position directly opposite to the point ‘ \[O\] ’. If the refractive index of the glass is \[1.5\] , find the position of the image formed. Also, draw the ray diagram for the formation of the image.

Answer 1

Hint:When light travels from the medium of one refractive index to another refractive index, light refraction occurs. We will use the lens formula for the phenomenon of refraction between two media of different index. Take \[{n_2}\] as the refractive index of air in the formula.

Formula used:
We will use this formula:
\[\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}\] …… (1)
Where,
\[{n_2}\] indicates the refractive index of air.
\[{n_1}\] indicates the refractive index of glass.
\[R\] indicates the radius of curvature of the glass sphere.
\[v\] indicates the image distance.
\[u\] indicates the object distance.

Complete step by step answer:
In the given question, we are supplied with the following data:
A point ‘ \[O\] ’ marked on the surface of a glass sphere. The diameter of the glass sphere is \[20\,{\text{cm}}\] .The point ‘ \[O\] ’ is viewed from the position directly opposite to that of the point ‘ \[O\] ’.The refractive index of the glass is \[1.5\] .We are asked to find the position of the image formed. We are also asked to draw the ray in support of the answer.

To begin with, we know that the refractive of air is \[1\] .
We have,
\[D = - 20\,{\text{cm}}\]
So, the radius of curvature is:
\[R = - 10\,{\text{cm}}\]
Now, we will substitute the required values in the equation (1) and we get:
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R} \\
\Rightarrow \dfrac{1}{v} - \dfrac{{1.5}}{{ - 20}} = \dfrac{{1 - 1.5}}{{ - 10}} \\
\Rightarrow \dfrac{1}{v} + \dfrac{{1.5}}{{20}} = \dfrac{{ - 0.5}}{{ - 10}} \\
\Rightarrow \dfrac{1}{v} = \dfrac{{0.5}}{{10}} - \dfrac{{1.5}}{{20}} \\
\Rightarrow \dfrac{1}{v} = - \dfrac{1}{{40}} \\
\therefore v = - 40\,{\text{cm}} \\$
The ray diagram in support of the answer is given below:

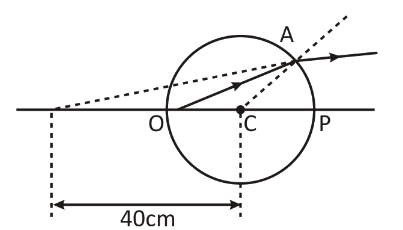
Hence, the position of the image is at \[40\,{\text{cm}}\] from the point of observation.

Note:While solving the problem, it is important to remember that the object distance is always taken as negative, according to the sign convention. This is because the object is always placed towards the left in the coordinate axis. Again, we need to keep in mind that the curvature radius is negative if the vertex lies to the right of the curvature centre. The curvature radius is positive if the vertex lies to the left of the curvature centre.