Question

A play top is in the form of a hemisphere surmounted on a cone. The diameter of the hemisphere is $3.6cm$. The total height of the play top is $4.2cm$. Find its total surface area.
$
  a)\,11.88\pi c{m^2} \\
  b)\,1.88\pi c{m^2} \\
  c)\,31.88\pi c{m^2} \\
  d)\,none\,\,of\,these \\
 $

Answer 1

Hint:The model consists of one hemispherical top and one cone that are joined together. The required dimensions of like diameter and height are given. So, the surface area of these individual shapes can be calculated.The total surface area of the figure will be equal to the sum of the curved surface area of the cone and curved surface area of the hemisphere only.

Complete step-by-step answer:
It is given that a play top is in the form of a hemisphere surmounted on a cone.
The diameter of the hemisphere is $3.6cm$.
Since the hemisphere and the cone are evenly joined, the diameter of the bases will be the same.
The total height of the play top is also given and is equal to $4.2cm$. The height is actually the sum of the radius of the hemisphere and height of the cone.

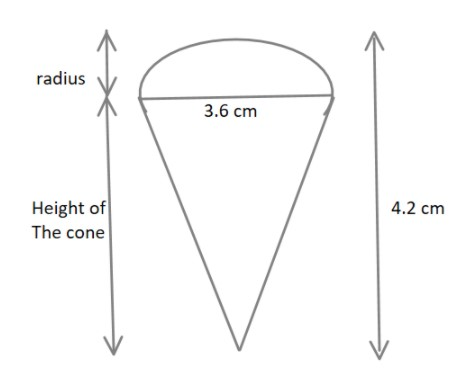
The radius $r$ of the hemisphere$ = \dfrac{{Diameter}}{2}$
$r = \dfrac{{3.6}}{2} = 1.8cm\,\,\,\,\,\,\,\,\,\, \to \left( 1 \right)$
Also, we need to calculate the height of the cone.
$
  Total\,height = Height\,of\,cone + r \\
  Height\,of\,cone(h) = 4.2 - 1.8 = 2.4cm\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to \left( 2 \right) \\
 $
Since we have the height as well as the radius of the cone so we can calculate length the curved region that is hypotenuse using Pythagoras Theorem,
$
  {(height)^2} + {(radius)^2} = {(hypotenuse)^2} \\
  {(h)^2} + {(r)^2} = {(l)^2} \\
  l = \sqrt {{h^2} + {r^2}} \\
  l = \sqrt {{{2.4}^2} + {{1.8}^2}} = \sqrt {5.76 + 3.24} \\
  l = \sqrt 9 \\
  l = 3\,\,\,\,\,\,\,\,\,\,\, \to \left( 3 \right) \\
 $
So the surface area of the body will be the area of the body exposed since the hemisphere and cone are joined together, the area of their bases will not be included in the total surface area of the play top.
$
  \therefore Total\,surface\,area = Curved\,surface\,area\,of\,cone + Curved\,surface\,area\,of\,hemisphere \\
$
Substituting the values from equations (1) , (2) and (3) we get,
$
Total\,surface\,area = \pi rl + 2\pi {r^2} \\
  Total\,surface\,area = \pi (1.8)(3) + 2\pi (1.8)(1.8) \\
  Total\,surface\,area = 5.4\pi + 6.48\pi \\
  Total\,surface\,area = 11.88\pi c{m^2} \\
 $

So, the correct answer is “Option A”.

Note:The student should understand the difference between the surface area of independent shapes and the surface area when these shapes are combined.And also should remember the formulas of curved surface areas of cone, hemisphere and other 3D shapes to solve these types of questions.