Question

A plane mirror is placed at the origin so that the direction ratios of its normal are $\left( {1, - 1,1} \right)$.A ray of light, coming along the positive direction of the x-axis, strikes the mirror. The direction cosines of the reflected ray are

A.$\dfrac{1}{3},\dfrac{2}{3},\dfrac{2}{3}$
B.$ - \dfrac{1}{3},\dfrac{2}{3},\dfrac{2}{3}$
C.$ - \dfrac{1}{3}, - \dfrac{2}{3}, - \dfrac{2}{3}$
D.$ - \dfrac{1}{3}, - \dfrac{2}{3},\dfrac{2}{3}$

Answer 1

Hint: We are given the direction ratio of the normal. So, we can find the direction cosine using the formula$\left( {\dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }},\dfrac{b}{{\sqrt {{a^2} + {b^2} + {c^2}} }},\dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}} \right)$. Then we can take the direction cosines of the reflected ray as 3 variables. Then we can equate the sum of the direction cosines of the incident and reflected rays to the direction cosines of the normal vector. Then we can solve the 3 variables to get the required direction cosines.

Complete step-by-step answer:
We can draw a diagram with the plane mirror at the origin. Let AO be the incident ray, ON be the normal of the plane mirror and OB be the reflected ray.

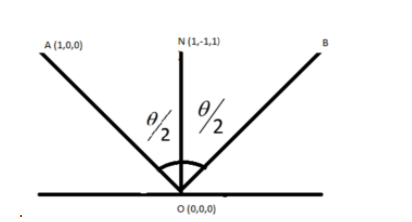
According to the law of reflection, we know that the angle of reflection is equal to the angle of incidence.
$ \Rightarrow \angle AON = \angle BON = \dfrac{\theta }{2}$
As the incident ray is coming along the positive x axis, its direction ratio can be written as $\left( {1,0,0} \right)$.
We know that if $\left( {a,b,c} \right)$are the direction ratios, the direction cosine is given by,
$\left( {\dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }},\dfrac{b}{{\sqrt {{a^2} + {b^2} + {c^2}} }},\dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}} \right)$

So, we get the direction cosine of the incident ray by substituting the values $\left( {1,0,0} \right)$ to the above equation.
$ \Rightarrow \left( {\dfrac{1}{{\sqrt {{1^2} + {0^2} + {0^2}} }},\dfrac{0}{{\sqrt {{1^2} + {0^2} + {0^2}} }},\dfrac{0}{{\sqrt {{1^2} + {0^2} + {0^2}} }}} \right)$
$ \Rightarrow \left( {1,0,0} \right)$
So, the direction cosine of the incident ray is$\left( {1,0,0} \right)$.
The direction ratio of the normal is given as, $\left( {1, - 1,1} \right)$.
Now we can find its direction cosine.
$ \Rightarrow \left( {\dfrac{1}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }},\dfrac{{ - 1}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }},\dfrac{1}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }}} \right)$
$ \Rightarrow \left( {\dfrac{1}{{\sqrt 3 }},\dfrac{{ - 1}}{{\sqrt 3 }},\dfrac{1}{{\sqrt 3 }}} \right)$
So, the direction cosine of the normal vector is $\left( {\dfrac{1}{{\sqrt 3 }},\dfrac{{ - 1}}{{\sqrt 3 }},\dfrac{1}{{\sqrt 3 }}} \right)$
From the two direction cosines, we can say that,
$\cos \left( {\dfrac{\theta }{2}} \right) = \dfrac{1}{{\sqrt 3 }}$
Let l, m, n be the direction cosines of the reflected ray. Then,
 $ \Rightarrow \left( {\dfrac{{l + 1}}{{2\cos \left( {\dfrac{\theta }{2}} \right)}},\dfrac{{m + 0}}{{2\cos \left( {\dfrac{\theta }{2}} \right)}},\dfrac{{n + 0}}{{2\cos \left( {\dfrac{\theta }{2}} \right)}}} \right) = \left( {\dfrac{1}{{\sqrt 3 }},\dfrac{{ - 1}}{{\sqrt 3 }},\dfrac{1}{{\sqrt 3 }}} \right)$
$ \Rightarrow \left( {\dfrac{{l + 1}}{{2 \times \dfrac{1}{{\sqrt 3 }}}},\dfrac{{m + 0}}{{2 \times \dfrac{1}{{\sqrt 3 }}}},\dfrac{{n + 0}}{{2 \times \dfrac{1}{{\sqrt 3 }}}}} \right) = \left( {\dfrac{1}{{\sqrt 3 }},\dfrac{{ - 1}}{{\sqrt 3 }},\dfrac{1}{{\sqrt 3 }}} \right)$
Now we can solve for l, m and n.
\[ \Rightarrow \dfrac{{l + 1}}{{\dfrac{2}{{\sqrt 3 }}}} = \dfrac{1}{{\sqrt 3 }}\]
On cross multiplication we get,
\[ \Rightarrow l + 1 = \dfrac{1}{{\sqrt 3 }} \times \dfrac{2}{{\sqrt 3 }} = \dfrac{2}{3}\]
On simplification we get,
\[ \Rightarrow l = \dfrac{2}{3} - 1 = - \dfrac{1}{3}\]
Now we can solve it.
\[ \Rightarrow \dfrac{{m + 0}}{{\dfrac{2}{{\sqrt 3 }}}} = \dfrac{{ - 1}}{{\sqrt 3 }}\]
On cross multiplication we get,
\[ \Rightarrow m = - \dfrac{1}{{\sqrt 3 }} \times \dfrac{2}{{\sqrt 3 }} = - \dfrac{2}{3}\]
Now we can solve for n.
\[ \Rightarrow \dfrac{{n + 0}}{{\dfrac{2}{{\sqrt 3 }}}} = \dfrac{1}{{\sqrt 3 }}\]
On cross multiplication we get,
\[ \Rightarrow n = \dfrac{1}{{\sqrt 3 }} \times \dfrac{2}{{\sqrt 3 }} = \dfrac{2}{3}\]
Therefore, the direction cosines of the reflected ray are $ - \dfrac{1}{3}, - \dfrac{2}{3},\dfrac{2}{3}$
So, the correct answer is option D.

Note: We must draw a diagram with the given plane, not in the three-dimensional space. The angle of incidence is the angle between the incident ray and the normal vector to the plane. The angle of reflection is the angle between the reflected ray and the normal vector to the plane. Direction cosines of a vector are the cosines of the angles that the vector makes with the positive x-axis, y-axis and z-axis. The sum of the square of direction cosines of a vector will be equal to one. The direction ratio is any number that is proportional to the direction cosines.