Question

A plane electromagnetic wave of frequency ${\text{25 M Hz}}$ travels in free space along the x-direction. At a particular point in space and time, $E = 6.3j{\text{ }}V/m.$ What is \[B\] at this point?

Answer 1

Hint: In this question, we have been provided with the value and direction of the electric field. Using this information we can calculate the value of the magnetic field. In order to do so, employ the formula containing the relation between electric field, magnetic field and the speed of light. By using proper units and substituting the values in the equation, we can easily decipher the answer.

Complete step by step solution:
The electric field and magnetic field are always perpendicular to each other. Hence, since the wave is travelling in the x-direction and the electric field is along the y-direction, the magnetic field will be along the z-direction.
This can be clearly understood from the diagram given below.
As mentioned in the question the wave is travelling along the x-direction. Also, the electric field is in the y-direction (j unit vector is mentioned in the question). Therefore combining the given information and that the electric field and magnetic field are always perpendicular to each other, we can determine the magnetic field to be along the z-direction.

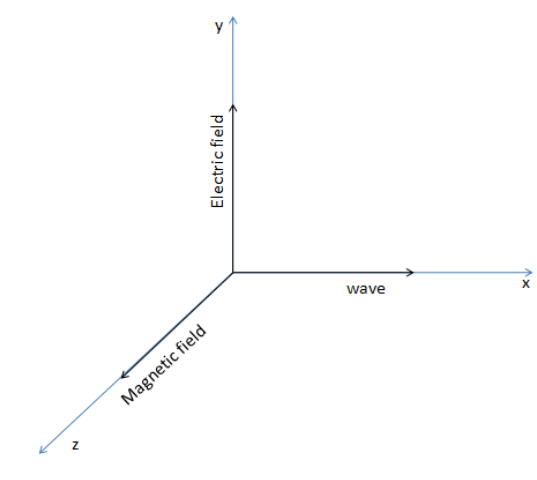
To solve the problem using the relation between the magnetic field, electric field, and speed of light. The relation is given by,
${\text{B = }}\dfrac{{\text{E}}}{{\text{c}}}$
Where B is the magnetic field, E is the electric field and c is the speed of light.
The given information is mentioned below
The frequency of the electromagnetic wave is equal to ${\text{25 MHz}}$
Electric field, ${E_y} = 6.3{\text{ V/m}}$
Speed of light, $c = 3 \times {10^8}{\text{ m/s}}$
We have to determine the value of the magnetic field at this point.
Therefore we get,
${{\text{B}}_z}{\text{ = }}\dfrac{{\text{E}}}{{\text{c}}}$
$ \Rightarrow {{\text{B}}_z}{\text{ = }}\dfrac{{6.3{\text{ V/m}}}}{{3 \times {{10}^8}{\text{ m/s}}}}$
$ \Rightarrow {{\text{B}}_z}{\text{ = }}2.1 \times {10^{ - 8}}T$
We know that ${10^{ - 6}}T = 1\mu T$
Therefore we get, ${{\text{B}}_z}{\text{ = 0}}{\text{.021}} \times \mu T$
The value of the magnetic field in the z-direction is ${{\text{B}}_z}{\text{ = 0}}{\text{.021}} \times \mu T$

Note:
Using the relation between electric field, magnetic field, and the speed of light we have been able to calculate the value of the magnetic field. The direction of the magnetic field was determined by using the knowledge that the electric field and magnetic field are always perpendicular to each other. Another important note is that not all values mentioned in the question need to be taken into consideration.