Question

A particle of positive charge q and mass m enters with velocity \[v\widehat{j}\] at the origin in a magnetic field \[B(-\overset\frown{k})\] which is present in the whole space. The charge makes a perfectly inelastic collision with an identical particle (having same charge) at rest but free to move at its maximum positive y-coordinate. After collision, the combined charge will move on trajectory (where \[r=\dfrac{mv}{qB}\]) –
\[\begin{align}
  & \text{A) }y=\dfrac{mv}{qB}x \\
 & \text{B) (}x+r{{)}^{2}}+{{(y-\dfrac{r}{2})}^{2}}=\dfrac{{{r}^{2}}}{4} \\
 & \text{C) (}x+r{{)}^{2}}+{{(y-\dfrac{r}{2})}^{2}}=\dfrac{{{r}^{2}}}{8} \\
 & \text{D) (}x-r{{)}^{2}}+{{(y+\dfrac{r}{2})}^{2}}=\dfrac{{{r}^{2}}}{4} \\
\end{align}\]

Answer 1

Hint: We need to understand the situation when a body inelastically collides with another body, here the charge in particular and the effect of the charges being in a magnetic field with a velocity imparted due to momentum to solve this problem.

Complete Solution:
We know that the inelastic collisions are a result of the sticking of the colliding particles without causing any complete transfer of the kinetic energy into the second body. The momentum after the collision is as a result of the cumulative mass of the two charges, which can be given as –
\[\begin{align}
  & \text{Momemtum before collision = Momentum after collision} \\
 & \Rightarrow mv+0=(m+m){{v}_{f}} \\
 & \therefore {{v}_{f}}=\dfrac{v}{2} \\
\end{align}\]
Now, we are told that the charge was initially moving with a velocity ‘v’ along the y-direction in a perpendicular magnetic field. We know that the Lorentz force acting on the particle will result in a circular path with a radius that can be given as –
\[{{r}_{before}}=\dfrac{mv}{qB}\]
The two charges after sticking together can be given as –
\[\begin{align}
  & {{r}_{after}}=\dfrac{2m{{v}_{f}}}{2qB} \\
 & \Rightarrow {{r}_{after}}=\dfrac{2m\dfrac{v}{2}}{2qB} \\
 & \therefore {{r}_{after}}=\dfrac{{{r}_{before}}}{2} \\
\end{align}\]

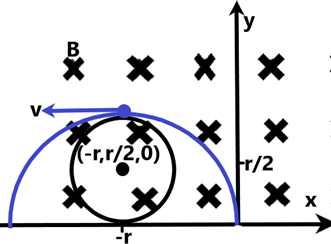
So, using the equation of a circle, we can find the final trajectory of the two charges as –
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}={{r}^{2}} \\
 & \Rightarrow {{(x+r)}^{2}}+{{(y-\dfrac{r}{2})}^{2}}={{(\dfrac{r}{2})}^{2}} \\
 & \therefore {{(x+r)}^{2}}+{{(y-\dfrac{r}{2})}^{2}}=\dfrac{{{r}^{2}}}{4} \\
\end{align}\]
This is the required trajectory for the system of charges in the given magnetic field.

Hence, the correct answer is option B.

Note:
We are told in the question that the two particles are free to move in the y-direction, but not in other directions. This is why we haven’t considered the change in the radius of circular motion along the x-direction for the final equation of the trajectory.