Question

A particle of mass m is thrown upwards from the surface of the earth, with a velocity u. The mass and the radius of the earth are, respectively, M and R. G is the gravitational constant and g is the acceleration due to gravity on the surface of the earth. The minimum value of u so that the particle does not return back to earth is
(A) $ \sqrt{\dfrac{2GM}{R}} $
(B) $ \sqrt{\dfrac{2GM}{{{R}^{2}}}} $
(C) $ \sqrt{2g{{R}^{2}}} $
(D) $ \sqrt{\dfrac{GM}{{{R}^{2}}}} $

Answer 1

Hint : Minimum speed with which a body has to be projected vertically upwards from the surface of the earth (or any other planet) so that it just crosses the gravitational field of earth and never returns on its own is known as ESCAPE SPEED.
As the speed of the projection is increased, the body rises up to a certain height and then falls back to earth. As the speed of projection is increased the body attains a greater height before falling. Finally, a stage reaches, when the speed is so large that it just crosses the gravitational field and will never return back to the earth on its own. The body is said to have escaped.

Complete step by step answer
Let earth be a perfect sphere of mass M, radius R, with centre at O. let a body of mass m to be projected from a point A on the surface of earth. Join OA and produce if further. Take two points P and Q at a distance x and (x + dx) from the center O of the earth.

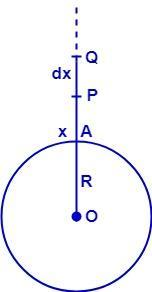
Gravitational Force of attraction at P is:
 $ F=\dfrac{GMm}{{{x}^{2}}} $
Work done in taking the body against gravitational attraction P and Q is:
 $ \begin{align}
  & dW=Fdx \\
 & =\dfrac{GMm}{{{x}^{2}}}dx \\
\end{align} $
Total work done in limits (x = R to x = $ \infty $ ):
 $ W=\int\limits_{R}^{\infty }{\dfrac{GMm}{{{x}^{2}}}}dx $
 $ \Rightarrow GMm{{\left[ \dfrac{{{x}^{-2+1}}}{-2+1} \right]}^{\infty }}_{R} $
 $ \Rightarrow -GMm{{\left[ \dfrac{1}{x} \right]}^{\infty }}_{R} $
 $ \Rightarrow -GMm\left[ \dfrac{1}{\infty }-\dfrac{1}{R} \right] $
 $ W=\dfrac{GMm}{R} $
 This work done is at the cost of K.E. given to the body at the surface of the earth. If $ {{v}_{e}} $ is the escape speed of the body projected from the surface of the earth, then
K.E. of the body = $ \dfrac{\text{1}}{\text{2}}\text{m}{{\text{v}}_{\text{e}}}^{\text{2}} $
 $ \dfrac{1}{2}m{{v}_{e}}^{2}=\dfrac{GMm}{R} $
Or
 $ {{v}_{e}}^{2}=\dfrac{2GM}{R} $
 $ {{v}_{e}}=\sqrt{\dfrac{2GM}{R}} $
Therefore option (A) is correct.

Additional Information
When the body goes just out of the gravitational field of the earth, then the total energy of the body at infinity is zero. Now $ {{v}_{e}} $ is called escape speed. Using law of conservation of mechanical energy for the body;
(P.E. + K.E) of the body at the surface of earth = total energy at infinity
 $ \Rightarrow -\dfrac{GMm}{R}+\dfrac{1}{2}m{{v}_{e}}^{2}=0 $
 $ \Rightarrow {{v}_{e}}^{2}=\dfrac{2GM}{R} $
 $ \Rightarrow {{v}_{e}}=\sqrt{\dfrac{2GM}{R}} $

Note
The value of escaped speed does not depend upon the mass (m) of the body and its angle of projection from the surface of earth or planet. it depends on the mass and radius of the planet from the surface of which the body is to be projected. If a body is projected from a planet with a speed v which is smaller than the escape speed, then the body will reach a certain height may either move in an orbit around the planet or may fall back to the planet. Make sure while projecting a body, the body should have higher speed as compared to escape speed.