Question

A particle is projected vertically upwards from the ground with an initial velocity $ u $ .
A. Find the maximum height, $ H, $ the particle will attain and time $ T $ that it will take to return to the ground.
B. What is the velocity when the particle returns to the ground?
C. What is the displacement and distance travelled by the particle during this time of the whole motion?

Answer 1

Hint: In order to find the solution for the given question, we need to know the equations of motion, that is $s=ut+\dfrac{1}{2}gt^2$.

Complete step by step answer:
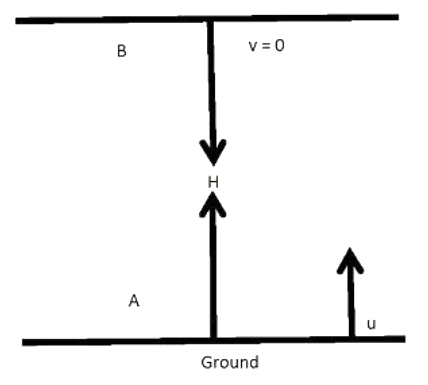
Let us consider that the motion is from $ A $ to $ B $
Since the initial position and final position are the same, the displacement, $ H $ in this case will be zero.
The value of initial velocity is given as $ u $ and the time taken is given as $ T $
Let the time taken to go from $ A $ to $ B $ be $ t $ .
From, Newton’s first equation of motion, we get,
 $ v = u - gt $
 $ \therefore t = \dfrac{u}{g} $
Now, we need to use Newton’s second equation we have,
 $ H = ut - \dfrac{1}{2}g{t^2} $
 $ H = u\dfrac{u}{g} - \dfrac{1}{2}g{\left( {\dfrac{u}{g}} \right)^2} = \dfrac{{{u^2}}}{{2g}} $ ……. (i)
Now, applying Newton’s second equation of motion, we get,
 $ s = ut + \dfrac{1}{2}g{t^2} $
After putting the values in the above equation, we can write it as,
 $ 0 = uT - \dfrac{1}{2}g{T^2} $
 $ \Rightarrow \dfrac{1}{2}g{T^2} = uT $
 $ \therefore T = \dfrac{{2u}}{g} $ …………….. (ii)
Therefore, the height attained is, $ H = \dfrac{{{u^2}}}{{2g}} $ and the time taken is, $ T = \dfrac{{2u}}{g} $
Step two
Now, while returning on the ground the velocity of the body will be the same but in the opposite direction.
Let us find the value.
Let us consider the velocity of the body while returning to the ground be $ v $ . Here, the initial velocity will be zero.
So, from Newton’s third equation of motion, we can write it as,
 $ {v^2} - {u^2} = 2gH $
 $ \Rightarrow {v^2} - 0 = - 2gH $
Now putting the values of height in the above equation from equation (i), we get,
 $ {v^2} = - 2g\dfrac{{{u^2}}}{{2g}} $
 $ \Rightarrow {v^2} = - {u^2} $
 $ \therefore v = - u $
Step three
Since the starting position and the final position are the same, the net displacement of the journey will be zero.
Now, the total distance covered is $ 2H = 2\dfrac{{{u^2}}}{{2g}} = \dfrac{{{u^2}}}{g} $
Hence, the total distance covered is $ \dfrac{{{u^2}}}{g} $

Note: Distance is defined as the total path of the ground covered. It does not depend on the path chosen. We define displacement as the shortest straight path covered between two points. The displacement depends on the path followed.