Question

A parallel beam of light is incident normally on a plane surface absorbing \[40\% \] of the light and reflecting the rest. If the incident beam carries \[60{\text{ }}watt\] power, the force exerted by it on the surface is:
${\text{A}}{\text{.}}\;\;3.2{\text{ }}x{\text{ }}{10^{ - 8}}N$
\[{\text{B}}{\text{.}}\;\;3.2{\text{ }}x{\text{ }}{10^{ - 7}}N\]
\[{\text{C}}{\text{. }}5.2{\text{ }}x{\text{ }}{10^{ - 7}}N\]
\[{\text{D}}{\text{. }}5.12{\text{ }}x{\text{ }}{10^{ - 8}}N\;\]

Answer 1

Hint:Calculate the power of reflected light as the absorption percentage is given.
Next, use the formula for the rate of momentum in terms of power and calculate this for both the incident ray and reflected ray. You need to remember the value of the speed of the light.
The change of rate of momentum, we can define it as Force.

Formula used:
The power of the reflected ray, ${P_r} = {P_i} \times \dfrac{{100 - 40}}{{100}}$
Where ${P_i}$ is the power of incident ray
For incident ray,
Momentum per second, ${p_i} = \dfrac{{{P_i}}}{c}$ , $c$ is the speed of light
For reflected ray,
Momentum per second, ${p_r} = \dfrac{{{P_r}}}{c}$.
Force exerted by the beam, $F = {p_r} - ( - {p_i})$ [ negative sign for opposite direction].

Complete step by step answer:
A parallel beam of light normally occurs on a surface and \[40\% \] of the light is absorbed by reflecting the rest.
Given the power of the incident ray is, ${P_i} = 60watt$
$\therefore $ The power of the reflected ray is, ${P_r} = {P_i} \times \dfrac{{100 - 40}}{{100}} = 0.6 \times 60 = 36watt$
The diagram is like,

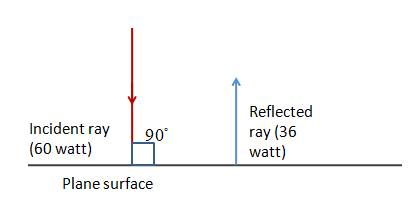
Now the relation between momentum per second with the power is, $p = \dfrac{P}{c}$ .
So, For incident ray,
Momentum per second, ${p_i} = \dfrac{{{P_i}}}{c}$ , $c = 3 \times {10^8}m/s$
$\therefore {p_i} = \dfrac{{60}}{{3 \times {{10}^8}}}$
$ \Rightarrow {p_i} = 2 \times {10^{ - 7}}N$
And, For reflected ray,
Momentum per second, ${p_r} = \dfrac{{{P_r}}}{c}$.
$\therefore {p_r} = \dfrac{{36}}{{3 \times {{10}^8}}}$
$ \Rightarrow {p_r} = 1.2 \times {10^{ - 7}}N$
The Force exerted by the beam, $F = {p_r} - ( - {p_i})$ [ negative sign for opposite direction].
$\therefore F = 1.2 \times {10^{ - 7}} - ( - 2 \times {10^{ - 7}})$
$ \Rightarrow F = 3.2 \times {10^{ - 7}}N$
So, if the beam carries \[{\text{60 watt}}\] power, the exerted of force will be \[3.2{\text{ }}x{\text{ }}{10^{ - 7}}N\].

Hence the right option is in option\[\left( B \right)\].

Note:The energy-momentum relation is $E = \dfrac{p}{c}$ , where $E$ is the energy and $p$ is the momentum. Since the power is defined by the,$P = E \times t$
So, the power per unit time is expressed as, $\dfrac{P}{t} = E = \dfrac{p}{c}$
So, we get the relation between the power and rate of the momentum.
We take the upward direction as a positive sign and the downward direction as a negative sign. Since the incident ray falling downward, We take the momentum of the incident ray negative.