Question

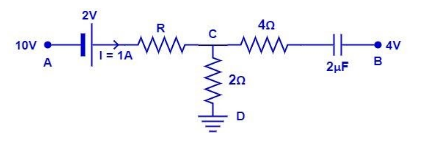
A network of resistances, cell and capacitor (C = 2µF) is shown in the adjoining figure. In steady state condition, the charge in this capacitor is Q while R is unknown resistance. What are the values of Q and R respectively?

Answer 1

Hint: Use the Kirchhoff’s Voltage law to the given circuit and calculate the charge and resistor on the capacitor.
Gustav Kirchhoff's Voltage Law is the second of his central laws we can use for circuit investigation. His voltage law expresses that for a closed loop series arrangement the logarithmic amount of the multitude of voltages around any closed loop in a circuit is equivalent to zero. This is on the grounds that a circuit circle is a closed path so no energy is lost.
All in all the logarithmic amount of all the possible potential differences around the circle should be equivalent to zero

Complete step by step solution

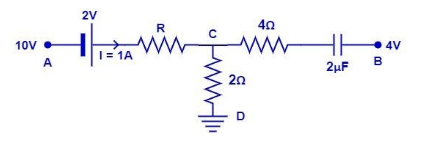
Given,
In the steady state, current through the capacitor is 1A.
Using Kirchhoff’s voltage law to the circuit ACD,
In ACD, $ {{V}_{1}}+{{V}_{2}}+{{V}_{3}}+{{V}_{4}}=0 $
 $ \begin{align}
  & 10-2-1\times R+1\times 2=0 \\
 & 8-R+2=0 \\
 & Or \\
 & R=10\Omega \\
\end{align} $
Potential difference across C and D
 $ \begin{align}
  & {{V}_{C}}-{{V}_{D}}=2-0\left( \because ,{{V}_{D}}=0V \right) \\
 & {{V}_{C}}=2V \\
\end{align} $
Potential difference across capacitor;
 $ \begin{align}
  & =4-2 \\
 & =2V \\
\end{align} $
Therefore, charge on the capacitor is:
 $ \begin{align}
  & Q=CV \\
 & Q=2\mu F\times 2V \\
 & Q=4\mu C \\
\end{align} $
Therefore, charge of the capacitor is $ 4\mu C $ and resistance R is $ 10\Omega $ .

Note
This thought by Kirchhoff is usually known as the Conservation of Energy, as moving around a closed loop, or circuit, you will wind up back to where you began in the circuit and hence back to a similar starting potential with no deficiency of voltage around the circle. Consequently any voltage drops around the circle should be equivalent to any voltage sources met en route.
So while applying Kirchhoff's voltage law to a particular circuit component, it is significant that we give uncommon consideration to the logarithmic signs, (+ and - ) of the voltage drops across components and the emf's of sources.