Answer
Verified471.6k+ views
Hint:Convert the inequality into linear equations and solve these equations to get the corner points.Plot the graph using these corner points of the feasible region and substitute in objective function and find the maximum and minimum value.
Complete step-by-step answer:
Here it is given that
\[Z = x + 2y\], subject to the constraints
\[\begin{array}{l}x + 2y \ge 100\\2x - y \le 0\\2x + y \le 200\end{array}\]
\[x,y \ge 0\] by graphical method.
We have to find the maximum and minimum value of \[Z\]
We have \[2x - y \le 0\] and \[x + 2y \ge 100\]
On solving equations \[2x - y = 0\] and \[x + 2y = 100\] we get point \[B\left( {20,40} \right)\]
Again we take \[2x - y \le 0\] and \[2x + y \le 200\]
On solving \[2x - y = 0\] and \[2x + y = 200\] we get \[C\left( {50,100} \right)\]
Now, equation \[2x + y = 200\]
We put \[x = 0\]
\[2\left( 0 \right) + y = 200\]
Then \[y = 200\]
So point is \[\left( {0,200} \right)\]
And equation \[x + 2y \ge 100\]
We put \[x = 0\]
\[0 + 2y \ge 100\]
Then \[y = 50\]
So point is \[\left( {0,50} \right)\]
We plot in graph
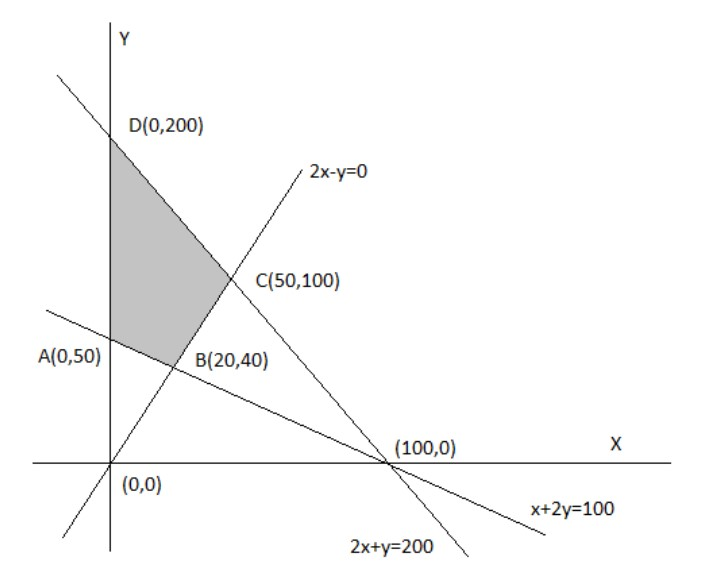
Therefore feasible region is shown by \[ABCDA\]
The corner points of the feasible region are \[A\left( {0,50} \right),{\rm{ }}B\left( {20,40} \right),{\rm{ }}C\left( {50,100} \right),{\rm{ }}D\left( {0,200} \right)\]
Let us evaluate the objective function Z at each corner points as shown below
At \[A\left( {0,50} \right),Z = 0 + 100 = 100\]
At \[B\left( {20,40} \right),Z = 20 + 80 = 100\]
At \[C\left( {50,100} \right),Z = 50 + 200 = 250\]
At \[D\left( {0,200} \right),Z = 0 + 400 = 400\]
Hence, Maximum value of \[Z\] is \[400\] at \[D\left( {0,200} \right)\] and minimum value of \[Z\] is \[100\] at \[A\left( {0,50} \right)\] and \[B\left( {20,40} \right)\].
Note:Linear programming is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships.The objective function means to maximize (or minimize) something.The constraints are the restrictions or limitations on the decision variables. They usually limit the value of the decision variables.Non-negativity restriction:For all linear programs, the decision variables should always take non-negative values.
$\text{b})$
Hint:Apply the row operation on the first row and to find determinant value expand along the first row and simplify it to get the required answer.
Complete step-by-step answer:
\[L.H.S = \] \[\Delta = \left| {\begin{array}{*{20}{c}}{b + c}&a&a\\b&{c + a}&b\\c&c&{a + b}\end{array}} \right|\]
Applying \[{R_1} \to {R_1} - {R_2} - {R_3}\]
Row1 is row1 subtract row2 and row 3
That is \[{R_1} \to {R_1} - {R_2} - {R_3}\]
\[\Delta = \left| {\begin{array}{*{20}{c}}{b + c - b - c}&{a - c - a - c}&{a - b - a - b}\\b&{c + a}&b\\c&c&{a + b}\end{array}} \right|\]
\[\Delta = \left| {\begin{array}{*{20}{c}}0&{ - 2c}&{ - 2b}\\b&{c + a}&b\\c&c&{a + b}\end{array}} \right|\]
From the sign chart, we see that 1 is in a positive position, \[( - 2c)\] is in a negative position and \[ - 2b\] is in a positive position. By putting the + or - in front of the element, it takes care of the sign adjustment when going from the minor to the cofactor.
Expanding determinant along
\[ = 0\left| {\begin{array}{*{20}{c}}{c + a}&b\\c&{a + b}\end{array}{\rm{ }}} \right| - ( - 2c)\left| {\begin{array}{*{20}{c}}b&b\\c&{a + b}\end{array}} \right| - 2b\left| {\begin{array}{*{20}{c}}b&{c + a}\\c&c\end{array}} \right|\]
Simplifying the determinant we get,
\[ = 0 - ( - 2c)\left| {{\rm{ }}\begin{array}{*{20}{c}}b&b\\c&{a + b}\end{array}} \right| - 2b\left| {\begin{array}{*{20}{c}}b&{c + a}\\c&c\end{array}} \right|\]
Solving the above determinant we get,
\[ = 0 + 2c\left( {b\left( {a + b} \right) - cb} \right) - 2b\left( {cb - c\left( {c + a} \right)} \right)\]
\[ = 2c\left( {ab + {b^2} - cb} \right) - 2b\left( {cb - {c^2} - ca} \right)\]
\[ = 2abc + 2abc + 2c{b^2} - 2c{b^2} - 2b{c^2} + 2b{c^2}\]
\[ = 4abc + 0\]
\[ = 4abc\]
\[ = R.H.S\]
\[L.H.S = R.H.S\]
Hence proved.
Note:The determinant of a square matrix A is denoted by "det A" or [(\left| A \right|\].Students should be careful while performing row or column operations and have to take care of the signs while expanding along row or column for finding the determinant.
Complete step-by-step answer:
Here it is given that
\[Z = x + 2y\], subject to the constraints
\[\begin{array}{l}x + 2y \ge 100\\2x - y \le 0\\2x + y \le 200\end{array}\]
\[x,y \ge 0\] by graphical method.
We have to find the maximum and minimum value of \[Z\]
We have \[2x - y \le 0\] and \[x + 2y \ge 100\]
On solving equations \[2x - y = 0\] and \[x + 2y = 100\] we get point \[B\left( {20,40} \right)\]
Again we take \[2x - y \le 0\] and \[2x + y \le 200\]
On solving \[2x - y = 0\] and \[2x + y = 200\] we get \[C\left( {50,100} \right)\]
Now, equation \[2x + y = 200\]
We put \[x = 0\]
\[2\left( 0 \right) + y = 200\]
Then \[y = 200\]
So point is \[\left( {0,200} \right)\]
And equation \[x + 2y \ge 100\]
We put \[x = 0\]
\[0 + 2y \ge 100\]
Then \[y = 50\]
So point is \[\left( {0,50} \right)\]
We plot in graph
Therefore feasible region is shown by \[ABCDA\]
The corner points of the feasible region are \[A\left( {0,50} \right),{\rm{ }}B\left( {20,40} \right),{\rm{ }}C\left( {50,100} \right),{\rm{ }}D\left( {0,200} \right)\]
Let us evaluate the objective function Z at each corner points as shown below
At \[A\left( {0,50} \right),Z = 0 + 100 = 100\]
At \[B\left( {20,40} \right),Z = 20 + 80 = 100\]
At \[C\left( {50,100} \right),Z = 50 + 200 = 250\]
At \[D\left( {0,200} \right),Z = 0 + 400 = 400\]
Hence, Maximum value of \[Z\] is \[400\] at \[D\left( {0,200} \right)\] and minimum value of \[Z\] is \[100\] at \[A\left( {0,50} \right)\] and \[B\left( {20,40} \right)\].
Note:Linear programming is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships.The objective function means to maximize (or minimize) something.The constraints are the restrictions or limitations on the decision variables. They usually limit the value of the decision variables.Non-negativity restriction:For all linear programs, the decision variables should always take non-negative values.
$\text{b})$
Hint:Apply the row operation on the first row and to find determinant value expand along the first row and simplify it to get the required answer.
Complete step-by-step answer:
\[L.H.S = \] \[\Delta = \left| {\begin{array}{*{20}{c}}{b + c}&a&a\\b&{c + a}&b\\c&c&{a + b}\end{array}} \right|\]
Applying \[{R_1} \to {R_1} - {R_2} - {R_3}\]
Row1 is row1 subtract row2 and row 3
That is \[{R_1} \to {R_1} - {R_2} - {R_3}\]
\[\Delta = \left| {\begin{array}{*{20}{c}}{b + c - b - c}&{a - c - a - c}&{a - b - a - b}\\b&{c + a}&b\\c&c&{a + b}\end{array}} \right|\]
\[\Delta = \left| {\begin{array}{*{20}{c}}0&{ - 2c}&{ - 2b}\\b&{c + a}&b\\c&c&{a + b}\end{array}} \right|\]
From the sign chart, we see that 1 is in a positive position, \[( - 2c)\] is in a negative position and \[ - 2b\] is in a positive position. By putting the + or - in front of the element, it takes care of the sign adjustment when going from the minor to the cofactor.
Expanding determinant along
\[ = 0\left| {\begin{array}{*{20}{c}}{c + a}&b\\c&{a + b}\end{array}{\rm{ }}} \right| - ( - 2c)\left| {\begin{array}{*{20}{c}}b&b\\c&{a + b}\end{array}} \right| - 2b\left| {\begin{array}{*{20}{c}}b&{c + a}\\c&c\end{array}} \right|\]
Simplifying the determinant we get,
\[ = 0 - ( - 2c)\left| {{\rm{ }}\begin{array}{*{20}{c}}b&b\\c&{a + b}\end{array}} \right| - 2b\left| {\begin{array}{*{20}{c}}b&{c + a}\\c&c\end{array}} \right|\]
Solving the above determinant we get,
\[ = 0 + 2c\left( {b\left( {a + b} \right) - cb} \right) - 2b\left( {cb - c\left( {c + a} \right)} \right)\]
\[ = 2c\left( {ab + {b^2} - cb} \right) - 2b\left( {cb - {c^2} - ca} \right)\]
\[ = 2abc + 2abc + 2c{b^2} - 2c{b^2} - 2b{c^2} + 2b{c^2}\]
\[ = 4abc + 0\]
\[ = 4abc\]
\[ = R.H.S\]
\[L.H.S = R.H.S\]
Hence proved.
Note:The determinant of a square matrix A is denoted by "det A" or [(\left| A \right|\].Students should be careful while performing row or column operations and have to take care of the signs while expanding along row or column for finding the determinant.