Questions & Answers
Question
AnswersA mass of $ 10Kg $ is at a point $ A $ on a table. It is moved to a point $ B $ . If the line joining $ A $ and $ B $ is horizontal, what is the work done on the object by the gravitational force? Explain your answer.
Answer
Verified92.4k+ views
Hint : Work is the measure of energy transfer when a force ( $ F $ ) moves an object through a distance ( $ d $ )
Force is an external agent capable of changing the state of rest or motion of a particular body. It has a magnitude and a direction.
Complete step by step answer
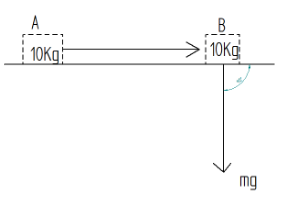
We have the mass kept on the table, $ m = 10Kg $ as shown in figure
Now the displacement of mass from A to B is horizontal
The force of gravitation acts vertically downward that is force is perpendicular to displacement
Then it is given by
$ W = FS\cos \theta $
We know the formula for force $ F $ after substituting formula the equation becomes
$ W = mg \times S \times \cos 90^\circ $
Here $ W $ becomes $ 0 $ because we know that $ \cos 90^\circ = 0 $ if $ \cos 90^\circ $ becomes $ 0 $ than the whole equation becomes $ 0 $
$ \therefore W = 0 $
Work done on the object by the gravitational force is $ 0 $ .
Note
The work done by gravitational force will be zero because whenever force is applied perpendicular to the surface the work done will be zero.
The direction of force is vertically downward and displacement is horizontal i. e, force and displacement are perpendicular to each other. So the work done will be zero
The gravitational force is a force that attracts any two objects with mass. We call the gravitational force attractive because it always tries to pull masses together, it never pushes them apart.
Force is an external agent capable of changing the state of rest or motion of a particular body. It has a magnitude and a direction.
Complete step by step answer
We have the mass kept on the table, $ m = 10Kg $ as shown in figure
Now the displacement of mass from A to B is horizontal
The force of gravitation acts vertically downward that is force is perpendicular to displacement
Then it is given by
$ W = FS\cos \theta $
We know the formula for force $ F $ after substituting formula the equation becomes
$ W = mg \times S \times \cos 90^\circ $
Here $ W $ becomes $ 0 $ because we know that $ \cos 90^\circ = 0 $ if $ \cos 90^\circ $ becomes $ 0 $ than the whole equation becomes $ 0 $
$ \therefore W = 0 $
Work done on the object by the gravitational force is $ 0 $ .
Note
The work done by gravitational force will be zero because whenever force is applied perpendicular to the surface the work done will be zero.
The direction of force is vertically downward and displacement is horizontal i. e, force and displacement are perpendicular to each other. So the work done will be zero
The gravitational force is a force that attracts any two objects with mass. We call the gravitational force attractive because it always tries to pull masses together, it never pushes them apart.