Question

A long straight wire carries a current i. Let ${{B}_{1}}$ be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section. Let ${{B}_{2}}$ be the magnetic field at this point due to this section only. Find the value of $d/l$ so that ${{B}_{2}}$ differs from ${{B}_{1}}$ by 1%.

Answer 1

Hint: Apply Biot Savart's law. Let us consider two magnetic fields ${{B}_{1}}\And {{B}_{2}}$.Given that the point P is at a distance d from the wire. Hence, here calculate the value of ${{B}_{1}}$. The value of ${{B}_{1}}$ is the product of permeability of free space and the current flowing through the wire to the product of two pi and the distance. Then calculate the magnetic field at ${{B}_{2}}$. Here also consider the same equation as the above. But here consider the sine of the angle also. Then by equating both ${{B}_{1}}\And {{B}_{2}}$we will get the value of $d/l$.

Complete answer:

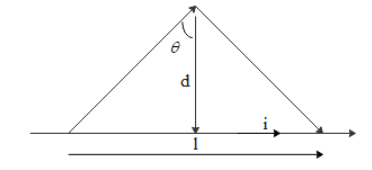
The magnetic field,
${{B}_{1}}=\dfrac{{{\mu }_{0}}I}{2\pi d}$
The magnetic field,
${{B}_{2}}=\dfrac{{{\mu }_{0}}I}{4\pi d}\left( \sin \theta +\sin \theta \right)$
$\Rightarrow {{B}_{2}}=\dfrac{{{\mu }_{0}}I}{4\pi d}\times 2\sin \theta $
$\Rightarrow {{B}_{2}}=\dfrac{{{\mu }_{0}}I}{4\pi d}\times 2\times \dfrac{l}{2\sqrt{{{d}^{2}}+{{\left( \dfrac{l}{2} \right)}^{2}}}}$
$\begin{align}
  & \dfrac{{{B}_{1}}-{{B}_{2}}}{{{B}_{1}}}=0.01 \\
 & \Rightarrow 1-\dfrac{{{B}_{2}}}{{{B}_{1}}}=0.01 \\
 & \Rightarrow \dfrac{{{B}_{2}}}{{{B}_{1}}}=1-0.01 \\
 & \Rightarrow \dfrac{{{B}_{2}}}{{{B}_{1}}}=0.99 \\
 & \\
\end{align}$
${{B}_{2}}={{B}_{1}}\times \dfrac{l}{2\sqrt{{{d}^{2}}+{{\left( \dfrac{l}{2} \right)}^{2}}}}$
 $\Rightarrow 0.99=\dfrac{l}{2\sqrt{{{d}^{2}}+{{\left( \dfrac{l}{2} \right)}^{2}}}}$
$\Rightarrow {{0.99}^{2}}=\dfrac{{{l}^{2}}}{4\left( {{d}^{2}}+\dfrac{{{l}^{2}}}{4} \right)}$
$\Rightarrow {{0.99}^{2}}\times 4\times \left( {{d}^{2}}+\dfrac{{{l}^{2}}}{4} \right)={{l}^{2}}$
$\Rightarrow {{0.99}^{2}}\times \left( {{d}^{2}}+\dfrac{{{l}^{2}}}{4} \right)=\dfrac{{{l}^{2}}}{4}$
$\Rightarrow {{0.99}^{2}}{{d}^{2}}=\dfrac{{{l}^{2}}}{4}\left( 1-{{0.99}^{2}} \right)$
$\Rightarrow {{0.99}^{2}}{{d}^{2}}=\dfrac{{{l}^{2}}}{4}\times 0.0199$
$\Rightarrow 197.005{{d}^{2}}={{l}^{2}}$
Rearranging the equation and taking the square root we get,
 $\begin{align}
  & \Rightarrow \dfrac{{{d}^{2}}}{{{l}^{2}}}=\dfrac{1}{197.005} \\
 & \therefore \dfrac{d}{l}=0.0712 \\
\end{align}$

Additional information:
The magnetic phenomena are universal in nature. The earth behaves as a magnetic field pointing in geographic south to north. When a bar magnet is suspended freely, it shows its pole in the north- south direction. The tip which points to geographic north is called north pole and tip which points to the geographic south is called the south pole of the magnet. There will be a repulsive force when north poles of two magnets are brought close together. We cannot isolate the north, or south poles of a magnet. That is, if we broke a bar magnet into two halves, we get two bar magnets of similar but weak properties.

Note:
Here Biot Savart’s law is employed. This law is used in case of constant electric current, that produces or generates a constant magnetic field. It also describes the direction , magnitude etc. of the magnetic field. It is also used to calculate the magnetic field intensity. Biot savart’s law thus relates magnetic fields with the current.