Question

A line d.c’s proportional to (2, 1, 2) meets each of the lines x = y + a = z and x + a = 2y = 2z. Then the coordinates of each of the points of intersection are given by
a) (3a, 2a, 3a);(a, a, 2a)
b) (3a, 2a, 3a);(a, a, a)
c) (3a, 3a, 3a);(a, a, a)
d) (2a, 3a, 3a);(2a, a, a)

Answer 1

Hint: Find the general points on both the lines by equating the given equations to two different constants. Suppose these general points as intersection points of both the lines with the line of d.c. (2, 1, 2). Get direction ratio of the line intersecting the given two lines by relation
$\left( \left( {{x}_{1}}-{{x}_{2}} \right),\left( {{y}_{1}}-{{y}_{2}} \right),\left( {{z}_{1}}-{{z}_{2}} \right) \right)$
Where\[\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)\] are two points on the line. Now, equate the ratio of given d.c. and calculated direction ratio, as the ratio of them should be equal and hence, get the intersection points. Direction cosine of any line is given as
$\left( \dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\dfrac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}} \right)$
Where, (a, b, c) are the direction ratio of the line.

Complete step-by-step answer:
As we know general representation of a line in three-dimension is given as
$\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}$ ……………………(i)
Where (a, b, c) is direction ratio of the line and line will pass through $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$
Now, coming to the question, we are given direction cosine of a line is proportional to (2, 1, 2) and the line is meeting the other two lines, whose equations are given as x = y + a = z, x + a = 2y = 2z and hence, we need to determine the intersection points of the line of direction cosine (2, 1, 2) with other two lines.
So, let us suppose line ${{L}_{1}},{{L}_{2}}$ can be represented as
${{L}_{1}}:\dfrac{x-0}{1}=\dfrac{y+a}{1}=\dfrac{z-0}{1}$ ……………….(ii)
${{L}_{2}}:\dfrac{x+a}{1}=\dfrac{2y}{1}=\dfrac{2z}{1}$ ………………….(iii)
Now, we can draw the diagram on the basis of the given information.
Let us suppose the line with the given direction cosine (2, 1, 2) is represented by L.

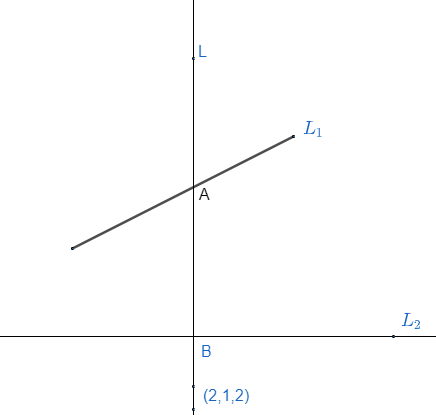
Where, line L is intersecting the lines ${{L}_{1}},{{L}_{2}}$at points A and B respectively. It means point A and B will also lie on line L as well.
Now, any general point on line L, can be given as we have
${{L}_{1}}:\dfrac{x-0}{1}=\dfrac{y+a}{1}=\dfrac{z-0}{1}$
Equate the above fractions to ${{k}_{1}}$, we get
$\dfrac{x-0}{1}=\dfrac{y+a}{1}=\dfrac{z-0}{1}={{k}_{1}}$
Now, we can get general point on line ${{L}_{1}}$by equating first three terms to ${{k}_{1}}$, so, we get
$\begin{align}
  & \to \dfrac{x-0}{1}={{k}_{1}}, \\
 & x={{k}_{1}} \\
 & \to \dfrac{y+a}{1}={{k}_{1}}, \\
 & y={{k}_{1}}-a \\
 & \to \dfrac{z-0}{1}={{k}_{1}}, \\
 & z={{k}_{1}} \\
\end{align}$
So, general point on line ${{L}_{1}}$ can be given as $\left( {{k}_{1}},{{k}_{1}}-a,{{k}_{1}} \right)$. Hence, suppose point A is given as $\left( {{k}_{1}},{{k}_{1}}-a,{{k}_{1}} \right)$for some value of ${{k}_{1}}$.
Similarly, equation of line ${{L}_{2}}$ is given as
 ${{L}_{2}}:\dfrac{x+a}{1}=\dfrac{2y}{1}=\dfrac{2z}{1}$
Now, we can equate the above fractions to \[{{k}_{2}}\]for getting the general point on the line ${{L}_{2}}$. So, we get
$\dfrac{x+a}{1}=\dfrac{2y}{1}=\dfrac{2z}{1}={{k}_{2}}$
So, we can get values of (x, y, z) as
$\begin{align}
  & \to \dfrac{x+a}{1}={{k}_{2}}, \\
 & x={{k}_{2}}-a \\
 & \to 2y={{k}_{2}}, \\
 & y=\dfrac{{{k}_{2}}}{2} \\
\end{align}$
Similarly
$2z={{k}_{2}}$
$z=\dfrac{{{k}_{2}}}{2}$
Hence, general point on the line ${{L}_{2}}$ is given as $\left( {{k}_{2}}-a,\dfrac{{{k}_{2}}}{2},\dfrac{{{k}_{2}}}{2} \right)$.
So, suppose point B as $\left( {{k}_{2}}-a,\dfrac{{{k}_{2}}}{2},\dfrac{{{k}_{2}}}{2} \right)$
Now, we can calculate the direction ratio of line L with the help of points A and B.
As we know we can get direction ratio of any line with the help of two points $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$lying on the line as
Direction ratio $=\left( {{x}_{1}}-{{x}_{2}},{{y}_{1}}-{{y}_{2}},{{z}_{1}}-{{z}_{2}} \right)$
Hence, direction ratio of line L can be calculated with the help of point A and B as
$=\left( {{k}_{1}}-\left( {{k}_{2}}-a \right) \right),\left( {{k}_{1}}-a-\dfrac{{{k}_{2}}}{2} \right),\left( {{k}_{1}}-\dfrac{{{k}_{2}}}{2} \right)$
$=\left( {{k}_{1}}-{{k}_{2}}+a,{{k}_{1}}-\dfrac{{{k}_{2}}}{2}-a,{{k}_{1}}-\dfrac{{{k}_{2}}}{2} \right)$…………….(iv)
Now, we know that the direction cosine of the line ‘L’ is given as (2, 1, 2). Also, we know direction cosine can be given with the help of direction ratio as

$\left(\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\dfrac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}} \right)$
Where a, b, c are the direction ratio of the line.
Hence, we get that the ratio of direction ratio and direction cosine will be the same, as the denominator of the direction cosine is the same.
So, the direction cosine (2, 1, 2) will be proportional to the direction ratio represented in equation (iv). So, we get
$\dfrac{{{k}_{1}}-{{k}_{2}}+a}{2}=\dfrac{{{k}_{1}}-\dfrac{{{k}_{2}}}{2}-a}{1}=\dfrac{{{k}_{1}}-\dfrac{{{k}_{2}}}{2}}{2},$
$\dfrac{{{k}_{1}}-{{k}_{2}}+a}{2}=\dfrac{2{{k}_{1}}-{{k}_{2}}-2a}{2}=\dfrac{2{{k}_{1}}-{{k}_{2}}}{4}$……………….(v)
Now, equating first two terms of the above equation, we get
$\begin{align}
  & \dfrac{{{k}_{1}}-{{k}_{2}}+a}{2}=\dfrac{2{{k}_{1}}-{{k}_{2}}-2a}{2}, \\
 & {{k}_{1}}-{{k}_{2}}+a=2{{k}_{1}}-{{k}_{2}}-2a \\
 & {{k}_{1}}+a=2{{k}_{1}}-2a \\
 & -{{k}_{1}}=-3a \\
\end{align}$
${{k}_{1}}=3a$………………….(vi)
Now, equation last two terms of the equation (v), we get
$\begin{align}
  & \dfrac{2{{k}_{1}}-{{k}_{2}}-2a}{2}=\dfrac{2{{k}_{1}}-{{k}_{2}}}{4} \\
 & 8{{k}_{1}}-4{{k}_{2}}-8a=4{{k}_{1}}-2{{k}_{2}} \\
 & 4{{k}_{1}}-8a=2{{k}_{2}} \\
\end{align}$
Putting ${{k}_{1}}=3a$ from equation (vi), we get
$\begin{align}
  & 4\left( 3a \right)-8a=2{{k}_{2}} \\
 & 2{{k}_{2}}=4a \\
\end{align}$
${{k}_{2}}=2a$………………(vii)
Now, we can get points A and B as
\[A\left( {{k}_{1}},{{k}_{1}}-a,{{k}_{1}} \right),B\left( {{k}_{2}}-a,\dfrac{{{k}_{2}}}{2},\dfrac{{{k}_{2}}}{2} \right)\]
So, we get points A and B from equations (vi) and (vii) as
A(3a, 3a – a, 3a),$B\left( 2a-a,\dfrac{2a}{2},\dfrac{2a}{2} \right),$
A(3a, 2a, 3a), B(a, a, a)
So, option (b) is the correct answer.

Note: Another approach for the question would be that, we can suppose the equation of line L as
$\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}$ and hence, find the general point on this line and therefore, by satisfying that point to line ${{L}_{1}},{{L}_{2}}$ , we can get the intersection points as well. Hence, it can be another approach.