Question

A light ray is travelling from air into a medium. The velocity of light in a medium is reduced to 0.75 times the velocity in air. Assume the angle of incidence i is very small, the deviation of the ray is:
A. i
B. $\dfrac{i}{3}$
C. $\dfrac{i}{4}$
D. $\dfrac{3i}{4}$

Answer 1

Hint: Using the fact that the refractive index of a medium is the ratio of the speed of light in air to the speed of light in medium, determine the refractive index of the medium. Then, approximate Snell’s law for small angles of incidence and refraction and substitute the appropriate values to determine the angle of refraction in terms of the angle of incidence. Following this, since we know that the angle of deviation is the difference between the incidence and the refractive angles, plug in the previously found result and arrive at the appropriate solution.

Formula used:
Snell’s law of refraction: $\dfrac{sin\;i}{sin\;r}=constant$
Refractive index $\mu = \dfrac{c}{v}$
Angle of deviation $\delta = i-r$

Complete step by step answer:
Let us begin by understanding the causes and the consequences of the reduction in the velocity of light as it travels through a medium denser than air.
When light rays travel across the boundary between two different media, they encounter a change in the velocity of their propagation through the second medium as a result of a change in the density of the particles constituting the media. This change in velocity is characterized by the bending of light rays, which we call as refraction.
Now, we have a parameter called the refractive index, which determines how fast light travels through a medium. It is given as:
$\mu = \dfrac{c}{v}$, where c is the speed of light in free space, and v is the speed of light in a medium. Thus, the refractive index is a dimensionless quantity and is only a ratio.
We can use this to define Snell’s law for a ray traversing from one medium to another of refractive indices $\mu_1$ and $\mu_2$ respectively, which would then be given as:
$\dfrac{sin\;i}{sin\;r}=\dfrac{\mu_2}{\mu_1}$
With this understanding, let us now look at the question.
Let the refractive index of air be $\mu_{air} = 1$ and the speed of light in air be $c\;ms^{-1}$
Let the refractive index of the medium be $\mu_{m}$ and the speed of light in the medium be $v\;ms^{-1}$

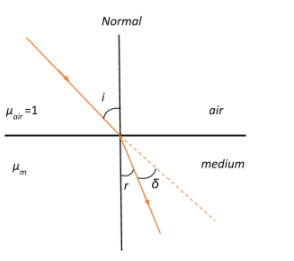
We know that $\mu_{m} = \dfrac{c}{v} \Rightarrow v = \dfrac{c}{\mu_{m}}$
We are given that the velocity of the light in the medium $v = 0.75\times c$
$\Rightarrow 0.75 \times c = \dfrac{c}{\mu_{m}}$
$\Rightarrow \mu_{m} = \dfrac{1}{0.75} = \dfrac{4}{3}$
Now, from Snell’s Law, we have:
$\dfrac{sin\;i}{sin\;r}=\dfrac{\mu_{m}}{\mu_{air}}$
We are given that the angle of incidence is very small, i.e., $sin\;i \approx i$
This means that the angle of refraction will also be small, i.e., $sin\;r \approx r$
Therefore, the expression now becomes:
$\dfrac{i}{r}=\dfrac{\mu_{m}}{\mu_{air}} \Rightarrow r = \dfrac{\mu_{air}}{\mu_{m}}.i = \dfrac{1}{\dfrac{4}{3}}.i = \dfrac{3i}{4}$
Now, the deviation of the light ray is the difference between its angle of incidence and angle of refraction, as shown in the diagram.
$\delta = i-r = i -\dfrac{3}{4}.i = \dfrac{4-3}{4}.i = \dfrac{i}{4} $
Therefore, the correct choice would be C. $\dfrac{i}{4}$

Note:
Remember that this phenomenon of refraction is constrained by the following laws that govern the behaviour of the incident light rays.
The incident ray and the refracted ray, along with the normal drawn at the point of incidence at the interface of two media, all lie in the same plane.
The refraction of light occurs in accordance with Snell’s law, which states that the ratio of the sine of the angle of incidence to the since of the angle of refraction is always a constant, i.e.,
$\dfrac{sin\;i}{sin\;r}=constant = \dfrac{\mu_2}{\mu_1} $
Thus, any tracing of paths of the incident, refracted and deviated rays and the values of the refractive indices of media must be consistent with the above two laws.