Question

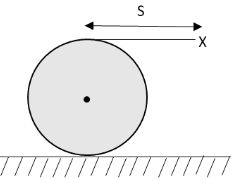
A large spool of rope lies on the ground as shown in the figure. The end, labelled X is pulled a distance \[S\] in the horizontal direction. The spool rolls without slipping. The centre of mass of the spool moves a distance

A.\[2S\]
B.\[S\]
C.\[S/2\]
D.\[S/4\]

Answer 1

Hint: Use the formula for linear velocity of an object in rotational motion. Also use the formula for linear velocity of an object in translational motion. Using these two formulae, determine the velocity of the centre of mass of the spool of rope and the topmost point X on the spool of rope. Take the ratio of the expressions of these two velocities and calculate the distance travelled by the centre of mass of the spool.

Formulae used:
The linear velocity \[v\] of an object in rotational motion is given by
\[v = R\omega \] …… (1)
Here, \[R\] is the radius of the circular path and \[\omega \] is the angular velocity of the object.
The linear velocity \[v\] of an object in translational motion is given by
\[v = \dfrac{x}{t}\] …… (2)
Here, \[x\] is the displacement of the object and \[t\] is the time required for the displacement.

Complete step by step answer:
We have given that the spool of the rope is lying on the ground and the end of the spool of rope is pulled in the horizontal direction by a distance \[S\].The spool of the rope while moving in the horizontal direction is rolling without slipping.Hence, the topmost point X on the circumference of the spool of the rope is in the translational as well as rotational motion and the centre of mass of the spool of the rope is only in translational motion.

Let \[v\] be the linear velocity of the centre of mass of spool of the rope which is given by
\[v = \dfrac{x}{t}\] …… (3)
Here, \[x\] is the displacement of the centre of mass of the spool of rope and \[t\] is the time required for the displacement.
Since the spool of the rope is rolling without slipping, the total velocity \[{v_{Total}}\] of the topmost point X on the circumference of the spool of rope is the sum of the linear velocity \[v\] due to translational motion and linear velocity \[R\omega \] due to rotational motion.
\[{v_{Total}} = v + R\omega \]
Here, \[\omega \] is the angular velocity of the point X on the spool of rope.

Substitute \[v\] for \[R\omega \] in the above equation.
\[{v_{Total}} = v + v\]
\[ \Rightarrow {v_{Total}} = 2v\]
Hence, the velocity of the topmost point X on the spool of rope is \[2v\].
Rewrite equation (2) for the total velocity of the point X.
\[2v = \dfrac{S}{t}\] …… (4)
Divide equation (3) by equation (4).
\[\dfrac{v}{{2v}} = \dfrac{{\dfrac{x}{t}}}{{\dfrac{S}{t}}}\]
\[ \Rightarrow \dfrac{1}{2} = \dfrac{x}{S}\]
\[ \therefore x = \dfrac{S}{2}\]
Therefore, the distance moved by the centre of mass is \[\dfrac{S}{2}\].

Hence, the correct option is C.

Note:The students should not forget to consider the rotational motion of the spool of the rope while calculating the total velocity of the topmost point X on the spool as the topmost point X is in translational as well as linear motion. If one forget to consider the velocity due to the rotational motion, the distance moved by the centre of mass of the spool will be the same as that of the point X which is not the correct answer.