Question

A ladder of mass $M$ and length $L$ is supported in equilibrium against a smooth vertical wall and a rough horizontal surface, as shown in figure. If $\theta $ is the angle of the angle of inclination of the rod with the horizontal, then calculate
(a). normal reaction of the wall on the ladder
(b). normal reaction of the ground on the ladder
(c). net force applied by the ground on the ladder

Answer 1

Hint: The ladder is in equilibrium against a wall, this means it is at rest or in uniform motion and no external forces act on it. We can apply Newton’s second law for forces acting in different directions and make equations. We can also apply equilibrium in its rotational motion and make equations for torque acting on it and solve the equations to calculate the value of forces.
Formulas used:
$\tau =F\times r$
${{N}_{1}}-F=0$
${{N}_{2}}-mg=0$

Complete answer:
The system of ladder is an isolated system, analyzing all the forces acting on it and resolving the forces into its components as follows

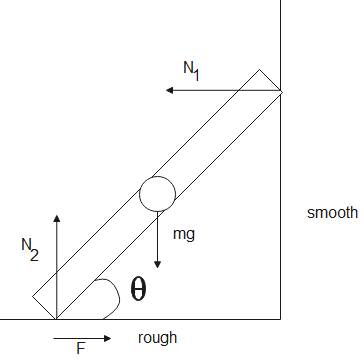
Since the ladder is on rest against the wall, the resultant of all forces acting on it will be 0.
Forces acting on the ladder in the x-direction
$\begin{align}
  & {{N}_{1}}-F=0 \\
 & \Rightarrow {{N}_{1}}=F \\
\end{align}$
Forces acting in the y-direction
$\begin{align}
  & {{N}_{2}}-mg=0 \\
 & \Rightarrow {{N}_{2}}=mg \\
\end{align}$
Now taking torque about point O, we have,

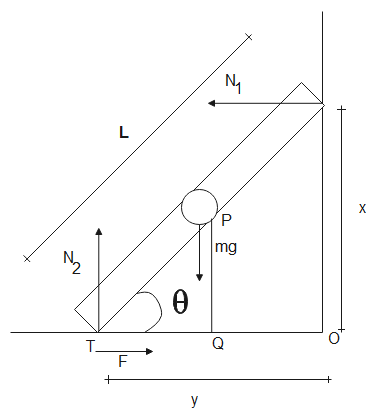
Since the ladder is in equilibrium, the net torque acting on it is 0.
Therefore, the torque is calculated as-
$\tau =F\times r$ - (2)
Here, $\tau $ is the torque
$F$ is the force acting on the ladder
$r$ is the distance from the axis
The axis is passing through point O
Distance of point of action of ${{N}_{1}}$ from the axis is calculated as-
From the triangle given in the above figure
$\begin{align}
  & \dfrac{x}{L}=\sin \theta \\
 & \Rightarrow x=L\sin \theta \\
\end{align}$
Distance of point of action of ${{N}_{2}}$ from the axis is calculated as-
$\begin{align}
  & \dfrac{y}{L}=\cos \theta \\
 & \Rightarrow y=L\cos \theta \\
\end{align}$
Distance of point of action of $mg$ from the axis is $\dfrac{L}{2}\cos \theta $
Therefore, from eq (2), the torque acting on the ladder is-
$\begin{align}
  & {{N}_{1}}L\sin \theta +{{N}_{2}}L\cos \theta -mg\dfrac{L}{2}\cos \theta =0 \\
 & \Rightarrow FL\sin \theta +mgL\cos \theta -mg\dfrac{L}{2}\cos \theta =0 \\
 & \Rightarrow FL\sin \theta +mg\dfrac{L}{2}\cos \theta =0 \\
 & \Rightarrow FL\sin \theta =-mg\dfrac{L}{2}\cos \theta \\
 & \Rightarrow F=-\dfrac{mg}{2}\cot \theta \\
\end{align}$
Substituting values for ladder in the above equation, we get,
$\therefore F=-\dfrac{Mg}{2}\cot \theta $
Therefore,
(a). The normal reaction of the wall on the ladder is $\dfrac{Mg}{2}\cot \theta $.
(b). The normal reaction of the ground on the ladder is $Mg$.
(c). the force applied by the ground on the ladder is $\dfrac{Mg}{2}\cot \theta $

Note:
The negative sign indicates that the force is opposite to the assumed direction. The normal reaction is perpendicular to the surfaces and by Newton’s third law, it acts equal and opposite on both the surfaces. The frictional force resists the motion of a body; it is applied by rough surfaces. When an object is in equilibrium, no net force or torque acts on it.