Question

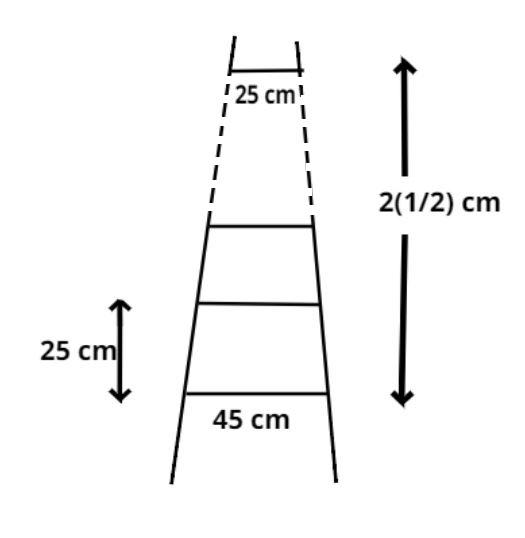
A ladder has rungs 25cm apart. The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are ${\text{2}}\dfrac{1}{2}{\text{m}}$apart, then what is the length of the wood required for the rungs?

Answer 1

Hint: -Length of the rungs decrease uniformly therefore they will form an A.P.

According to the question it is given that the rungs are 25cm apart and the top and bottom rungs are ${\text{2}}\dfrac{1}{2}{\text{m}}$apart.
$ \Rightarrow {\text{2}}\dfrac{1}{2}m = \dfrac{5}{2}m = \dfrac{{500}}{2}cm = 250cm.\left[ {\because {\text{ 1m = 100cm}}} \right]$
$\therefore $Total number of rungs${\text{ = }}\dfrac{{{\text{Distance between total rungs}}}}{{{\text{Distance between two rungs}}}} + 1$, (plus one because of the bottom rung and thereafter all rungs are 25 cm apart).
$\therefore $Total number of rungs${\text{ = }}\dfrac{{250}}{{25}} + 1 = 11$
Now as the length of the rungs decrease uniformly therefore they will form an A.P.
So the A.P becomes $\left( {45,.................,25} \right)$
So, first term $\left( {{a_1}} \right)$of an A.P${\text{ = 45}}$, last term $\left( {{a_n}} \right)$of an A.P${\text{ = 25}}$, and number of terms in this A.P$ = 11$
Now, as we know last term of this series is written as
${a_n} = {a_1} + \left( {n - 1} \right)d$, Where d is the common difference.
$ \Rightarrow d = \dfrac{{{a_n} - {a_1}}}{n} + 1 = \dfrac{{25 - 45}}{{11}} + 1 = \dfrac{{ - 20}}{{11}} + 1 = \dfrac{{ - 9}}{{11}}$
So, the length of the rungs decrease uniformly by $\dfrac{{ - 9}}{{11}}cm$
The length of the wood required for the rungs equals the sum of all the terms of this A.P
${S_n} = 45 + \left( {45 - \dfrac{9}{{11}}} \right) + \left( {45 - \dfrac{9}{{11}} - \dfrac{9}{{11}}} \right) + .............. + 25$
Therefore sum of this A.P${\text{ = }}{{\text{S}}_n} = \dfrac{n}{2}\left( {{a_1} + {a_l}} \right)$
$ \Rightarrow {{\text{S}}_n} = \dfrac{{11}}{2}\left( {45 + 25} \right) = 11 \times 35 = 385cm$
Therefore the length of the wood required for the rungs${\text{ = 385cm}}$.

Note: -In such types of questions first find out the total numbers of rungs, then the key concept is that the length of the rungs decrease uniformly so, they will form an A.P so, the length of the wood required for the rungs equals the sum of all the terms of this A.P, so apply the formula of sum of an A.P which is stated above, we will get the required answer.