Question

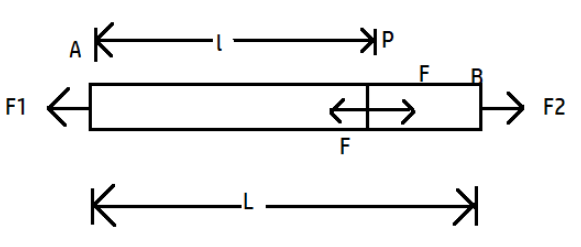
A homogeneous rod of length L is acted upon by the two forces \[{{F}_{1}}\] and \[{{F}_{2}}\] applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where force \[{{F}_{1}}\] is applied?

 (A) \[\dfrac{{{F}_{2}}-{{F}_{1}}}{2L}\]
(B) \[\dfrac{({{F}_{2}}-{{F}_{1}})l}{L}\]
(C) \[\dfrac{({{F}_{2}}-{{F}_{1}})l}{L}+{{F}_{1}}\]
(D) \[\dfrac{({{F}_{2}}-{{F}_{1}})l}{L}+{{F}_{2}}\]

Answer 1

Hint: We are given in the question that the rod is homogeneous which means mass is uniformly throughout and two forces act. We are not given which force is greater in magnitude. We need to find the magnitude

Complete step by step answer:
Let m be mass per unit length and since it is not given which force is greater in magnitude, assuming \[{{F}_{2}}<{{F}_{1}}\]
So, the system will move towards the left. Let a be the acceleration of the system
For AP:
Length=l
Mass of this length is ml
Applying Newton’s second law \[(ml)a={{F}_{1}}-F\]-------(1)
For PB:
\[\Rightarrow m(L-1)a=F-{{F}_{2}}\]-----(2)
Divide eq (2) by (1) we get, \[\dfrac{F-{{F}_{2}}}{{{F}_{1}}-F}=\dfrac{L-1}{l}\]
Cross multiplying, we get,
\[\begin{align}
&\Rightarrow (\dfrac{L}{l}-1){{F}_{1}}-(\dfrac{L}{l}-1)F=F-{{F}_{2}} \\
&\Rightarrow F=(1-\dfrac{l}{L}){{F}_{1}}+{{F}_{2}}(\dfrac{l}{L}) \\
&\therefore F=\dfrac{({{F}_{2}}-{{F}_{1}})l}{L}+{{F}_{1}} \\
\end{align}\]

Thus, the correct option is (C).

Additional Information:
when more than one force acts on any system then we have to add all the forces vectorially using either triangle law of vector addition or parallelogram law of vector addition.

Note: Here we have assumed that one force is greater than another to find the net force and then has applied Newton’s second law. The forces were opposite in direction so resultant force was towards the left. We are not given with any numerical values, we have to arrive at the solution algebraically.