Question

A highly rigid cubical block A of small mass \[M\] and side \[L\] is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity \[\eta \] such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force \[F\] is applied perpendicular to one of a side faces of A. After the force is withdrawn, block A executes small oscillations, the time period of which is given by
A. \[2\pi \sqrt {M\eta L} \]
B. \[2\pi \sqrt {M\eta /L} \]
C. \[2\pi \sqrt {ML/\eta } \]
D. \[2\pi \sqrt {M/\eta L} \]

Answer 1

Hint: Use the formula for modulus of rigidity of the material of an object. Also use the formula for area of a cube. Use the expression for Newton’s second law of motion and also the formula for time period of a simple pendulum. From all these formulae, determine the amplitude of small oscillation of the block and acceleration of the block and substitute these values in the formula for time period.

Formulae used:
The modulus of rigidity \[\eta \] is given by
\[\eta = \dfrac{F}{{A\theta }}\] …… (1)
Here, \[F\] is the shearing force, \[A\] is the area on which the shearing force is applied and \[\theta \] is the angle by which the surface of the object on which shearing force is applied displaces from its original position.
The area \[A\] of a cube is given by
\[A = {L^2}\] …… (2)
Here, \[L\] is the side of the cube.
The expression for Newton’s second law of motion is
\[{F_{net}} = ma\] …… (3)
Here, \[{F_{net}}\] is net force acting on the object, \[m\] is mass of the object and \[a\] is acceleration of the object.
The time period \[T\] of a simple pendulum is
\[T = 2\pi \sqrt {\dfrac{L}{g}} \] …… (4)
Here, \[L\] is the length of the simple pendulum and \[g\] is acceleration due to gravity.

Complete step by step answer:
We have given that a rigid cubical block of mass \[M\] and side \[L\] is placed on the upper side of another cubical block B of less rigidity \[\eta \] than block A. A small force \[F\] is applied to the one side of block A and due to this force the block A starts oscillating.

The diagram of the block A when it starts oscillating is as follows:

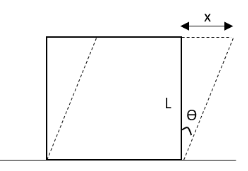
From the above figure, we can see that the amplitude of oscillation of the block is \[x\]. The angle by which the block displaces from its original position is \[\theta \]. Let us determine sine of the angle \[\theta \] from the above diagram.
\[\sin \theta = \dfrac{x}{L}\]

As the angle \[\theta \] is very small, we can write \[\sin \theta \approx \theta \].
\[ \Rightarrow \theta = \dfrac{x}{L}\]
Rearrange equation (1) for the restoring force \[F\].
\[ \Rightarrow F = \eta A\theta \]
Substitute \[{L^2}\] for \[A\] and \[\dfrac{x}{L}\] for \[\theta \] in the above equation.
\[ \Rightarrow F = - \eta \left( {{L^2}} \right)\left( {\dfrac{x}{L}} \right)\]
\[ \Rightarrow F = \eta xL\]

Let us now determine the acceleration \[a\] of the oscillation block. Rearrange equation (3) for acceleration of the block.
\[a = \dfrac{{{F_{net}}}}{m}\]
Substitute \[F\] for \[{F_{net}}\] and \[M\] for \[m\] in the above equation.
\[a = \dfrac{F}{M}\]
Substitute \[\eta xL\] for \[F\] in the above equation.
\[a = \dfrac{{\eta xL}}{M}\]

Let us now calculate the time period of oscillation of the block using equation (4).Substitute \[x\] for \[L\] and \[a\] for \[g\] in equation (4).
\[T = 2\pi \sqrt {\dfrac{x}{a}} \]
Substitute \[\dfrac{{\eta xL}}{M}\] for \[a\] in the above equation.
\[T = 2\pi \sqrt {\dfrac{x}{{\dfrac{{\eta xL}}{M}}}} \]
\[ \therefore T = 2\pi \sqrt {\dfrac{M}{{\eta L}}} \]
Therefore, the time period of oscillation of the block is \[2\pi \sqrt {\dfrac{M}{{\eta L}}} \].

Hence, the correct option is D.

Note:The students may think that we have not used acceleration due to gravity in the formula for the time period of the block. Instead of acceleration due to gravity, we have used acceleration of the block during the small oscillation. But the students should keep in mind that the block oscillating is not an actual pendulum. It is oscillating that’s why we have used formulas for time periods of simple pendulums. But the block has its own acceleration.