A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1m, then find the volume of the iron used to make the tank?
Answer
Verified360.9k+ views
Hint – The hemispherical tank is made up of iron sheet whose thickness is given to us thus the outer radius of this hemispherical tank will be the sum of the thickness and the inner radius. Use this concept to reach the right solution.
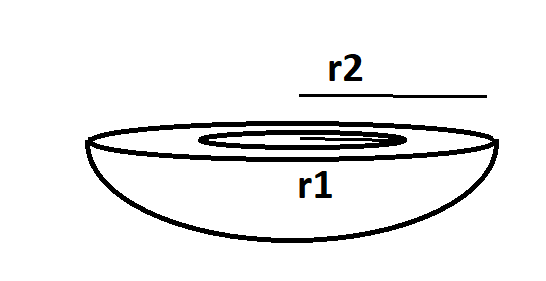
Inner radius of tank is given as ${r_1} = 1{\text{ }}m$
Thickness of the iron sheet of which the hemispherical tank is made up of is 1 cm = 0.01 m (1m = 100 cm)
Thus
Outer radius = Thickness of iron sheet + Inner radius of tank………………………. (1)
Using equation (1)
Outer radius ${r_2}$ = 1 + 0.01 = 1.01 m
Volume of iron used = Volume of the tank of outer radius – Volume of tank of inner radius……… (2)
Now the volume of hemisphere $V = \dfrac{2}{3}\pi {r^3}$ ………………. (3)
Using equation (3) in equation (2) we get
Volume of iron used = $\dfrac{2}{3}\pi {r_2}^3 - \dfrac{2}{3}\pi {r_1}^3$
$ \Rightarrow \dfrac{2}{3}\pi \left( {{r_2}^3 - {r_1}^3} \right)$
On putting the values we get
$\begin{gathered}
\Rightarrow \dfrac{2}{3} \times \dfrac{{22}}{7} \times \left( {{{\left( {1.01} \right)}^3} - {1^3}} \right) \\
\Rightarrow 0.06343{\text{ c}}{{\text{m}}^3} \\
\end{gathered} $
Thus volume of iron used is 0.06343 $c{m^3}$
Note – Whenever we face such a type of problem statement the important basic that we need to take care of is some sides may be in different units as compared to others, thus their conversion into the same units is mandatory to reach the right answer.
Inner radius of tank is given as ${r_1} = 1{\text{ }}m$
Thickness of the iron sheet of which the hemispherical tank is made up of is 1 cm = 0.01 m (1m = 100 cm)
Thus
Outer radius = Thickness of iron sheet + Inner radius of tank………………………. (1)
Using equation (1)
Outer radius ${r_2}$ = 1 + 0.01 = 1.01 m
Volume of iron used = Volume of the tank of outer radius – Volume of tank of inner radius……… (2)
Now the volume of hemisphere $V = \dfrac{2}{3}\pi {r^3}$ ………………. (3)
Using equation (3) in equation (2) we get
Volume of iron used = $\dfrac{2}{3}\pi {r_2}^3 - \dfrac{2}{3}\pi {r_1}^3$
$ \Rightarrow \dfrac{2}{3}\pi \left( {{r_2}^3 - {r_1}^3} \right)$
On putting the values we get
$\begin{gathered}
\Rightarrow \dfrac{2}{3} \times \dfrac{{22}}{7} \times \left( {{{\left( {1.01} \right)}^3} - {1^3}} \right) \\
\Rightarrow 0.06343{\text{ c}}{{\text{m}}^3} \\
\end{gathered} $
Thus volume of iron used is 0.06343 $c{m^3}$
Note – Whenever we face such a type of problem statement the important basic that we need to take care of is some sides may be in different units as compared to others, thus their conversion into the same units is mandatory to reach the right answer.
Last updated date: 19th Sep 2023
•
Total views: 360.9k
•
Views today: 6.60k
