Question

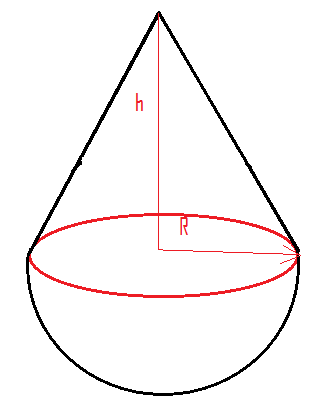
A hemisphere and a solid cone of the same density have a common base. The center of mass of the common structure coincides with the center of the common base. If R is the radius of hemisphere and h is the height of the cone, then:
(A). $\dfrac{h}{R} = \sqrt 3 $
(B). $\dfrac{h}{R} = \dfrac{1}{{\sqrt 3 }}$
(C). $\dfrac{h}{R} = 3$
(D). $\dfrac{h}{R} = \dfrac{1}{3}$

Answer 1

Hint: The center of mass of the body is the position which is defined as the average position of all parts of the system which are weighted according to their masses. For rigid bodies, the center of the body is located at the centroid of the body.

The formula used: To solve this type of question we use the following formula.
Volume of hemisphere $V = \dfrac{2}{3}\pi {r^3}$
Volume of cone $V = \dfrac{1}{3}\pi {r^2}h$
Mass= density × volume.
${\text{The center of mass = }}\dfrac{{{{\text{m}}_{\text{1}}}{{\text{y}}_{\text{1}}}{\text{ + }}{{\text{m}}_{\text{2}}}{{\text{y}}_{\text{2}}}}}{{{{\text{m}}_{\text{1}}}{\text{ + }}{{\text{m}}_2}}}$
Where, ${{\text{m}}_{\text{1}}}{\text{,}}{{\text{m}}_{\text{2}}}$ are the masses and ${{\text{y}}_{\text{1}}}{\text{,}}{{\text{y}}_{\text{2}}}$ are the position of masses from the centroid.

 Complete step by step answer:
Let’s the cones and hemisphere are made of the same material. If so then the density of the cone is equal to the density of the hemisphere. We can write it as follows,

${{\text{d}}_{\text{C}}}{\text{ = }}{{\text{d}}_{\text{H}}}$
Where, ${{\text{d}}_{\text{C}}}$ is the density of the cone and ${{\text{d}}_{\text{H}}}$ is the density of the hemisphere.
Since, \[{\text{d = }}\dfrac{{\text{m}}}{{\text{V}}}\] ……………….(1)
Equation (1) can be written as
$\dfrac{{{{\text{M}}_{\text{c}}}}}{{{{\text{V}}_{\text{c}}}}}{\text{ = }}\dfrac{{{{\text{M}}_{\text{H}}}}}{{{{\text{V}}_{\text{H}}}}}$ ………………...(2)
Rearrange the equation (2) as follows,
$\dfrac{{{{\text{M}}_{\text{c}}}}}{{{{\text{M}}_{\text{H}}}}}{\text{ = }}\dfrac{{{{\text{V}}_{\text{c}}}}}{{{{\text{V}}_{\text{H}}}}}$ ………………... (3)
We know that the volume of the cone is given as $V = \dfrac{1}{3}\pi {r^2}h$ and the volume of the hemisphere is given as $V = \dfrac{2}{3}\pi {r^3}$
Let's substitute the values of volume of cone and hemisphere in the equation (3) we get,
$\dfrac{{{{\text{M}}_{\text{c}}}}}{{{{\text{M}}_{\text{H}}}}}{\text{ = }}\dfrac{{\dfrac{1}{3}\pi {R^2}h}}{{\dfrac{2}{3}\pi {R^3}}}$
On canceling the π, r, and 3 from the denominator and numerator we get,
\[\dfrac{{{{\text{M}}_{\text{c}}}}}{{{{\text{M}}_{\text{H}}}}}{\text{ = }}\dfrac{h}{{2R}}\]
Thus on rearranging the equation for the mass of cone we get,
\[{{\text{M}}_{\text{c}}}{\text{ = }}\dfrac{h}{{2R}}{{\text{M}}_{\text{H}}}\]
The Center of the body lies at the point at the centroid of the body. The centroid of the body is at the origin such that the value of the y axis is zero.
Let's use the center of the body to determine the height of the body.
${\text{The center of mass = }}\dfrac{{{{\text{m}}_{\text{1}}}{{\text{y}}_{\text{1}}}{\text{ + }}{{\text{m}}_{\text{2}}}{{\text{y}}_{\text{2}}}}}{{{{\text{m}}_{\text{1}}}{\text{ + }}{{\text{m}}_2}}}$
${\text{The center of mass = }}\dfrac{{{{\text{m}}_C}{{\text{y}}_{\text{1}}}{\text{ + }}{{\text{m}}_{\text{H}}}{{\text{y}}_{\text{2}}}}}{{{{\text{m}}_{\text{C}}}{\text{ + }}{{\text{m}}_{\text{H}}}}}$
The y-axis for the cone is,${{\text{y}}_{\text{1}}}{\text{ = }}\dfrac{{\text{h}}}{{\text{4}}}$
The y-axis for hemisphere is, ${{\text{y}}_2}{\text{ = }}\dfrac{{{\text{ - 3hR}}}}{8}$
Let's substitute these values in the center of mass. We get,
${\text{The center of mass = }}\dfrac{{{{\text{m}}_C}{{\text{y}}_{\text{1}}}{\text{ + }}{{\text{m}}_{\text{H}}}{{\text{y}}_{\text{2}}}}}{{{{\text{m}}_{\text{C}}}{\text{ + }}{{\text{m}}_{\text{H}}}}}$
${\text{0 = }}\dfrac{{{{\text{m}}_{\text{H}}} \times \dfrac{h}{{2R}} \times \dfrac{h}{4}{\text{ + }}{{\text{m}}_{\text{H}}} \times \left( {\dfrac{{ - 3R}}{8}} \right)}}{{{{\text{m}}_{\text{H}}} \times \dfrac{h}{{2R}} + {{\text{m}}_{\text{H}}}}}$
Since we know that \[{{\text{M}}_{\text{c}}}{\text{ = }}\dfrac{h}{{2R}}{{\text{M}}_{\text{H}}}\]
On further simplification we get,
\[{\text{0 = }}\dfrac{{\dfrac{{{h^2}}}{{8R}}\left( {\dfrac{{ - 3R}}{8}} \right){{\text{m}}_{\text{H}}}}}{{(\dfrac{h}{{2R}} + 1){{\text{m}}_{\text{H}}}}}\]
We get,
$\dfrac{{{{\text{h}}^{\text{2}}}}}{{{\text{8R}}}}{\text{ - }}\dfrac{{{\text{3R}}}}{{\text{8}}}{\text{ = 0}}$
$\dfrac{{{{\text{h}}^{\text{2}}}}}{{{\text{8R}}}}{\text{ = }}\dfrac{{{\text{3R}}}}{{\text{8}}}$
${{\text{h}}^{\text{2}}}{\text{ = 3}}{{\text{R}}^{\text{2}}}$
Therefore, ${\text{h = }}\sqrt {\text{3}} {\text{R}}$
Hence, option (A) is the correct option.

Note:
The center of mass (distribution of mass in space) is the unique point where the weighted relative position of the distributed mass sums to zero, that is it is the point at which the object can be balanced.
The Center of mass is the point to which a force may be applied to cause a linear acceleration without an angular acceleration.
The center of mass is useful because problems can often be simplified by creating a collection of masses as one mass at their common center of mass.