Question

A group of 123 workers went to a canteen for coffee, ice-cream and tea. 42 workers took ice-cream, 36 took tea and 30 took coffee, 15 workers purchased ice-cream and tea, 10 ice-cream and coffee and 4 coffee and tea but not ice-cream, while 11 took ice-cream and tea but not coffee. Determine how many workers did not purchase anything?

Answer 1

Hint: We will proceed in this problem by making a venn diagram of the problem.
Let consider three sets i.e., $C$, $I$ and $T$ which represents the workers purchasing coffee, ice-cream and tea respectively.

Complete step-by-step answer:

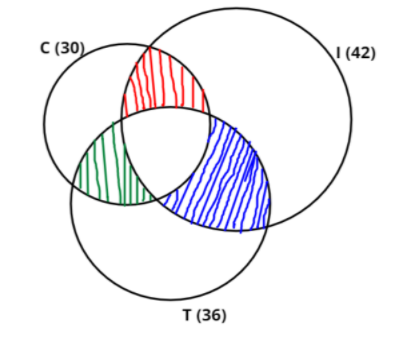
\[{\text{Total number of workers}} = 123\]
Number of workers purchasing ice-cream, $n\left( I \right) = 42$
Number of workers purchasing tea, $n\left( T \right) = 36$
Number of workers purchasing coffee, $n\left( C \right) = 30$
Number of workers purchasing ice-cream and tea, $n\left( {I \cap T} \right) = 15$
Number of workers purchasing ice-cream and coffee, $n\left( {I \cap C} \right) = 10$
Number of workers purchasing only ice-cream and tea but not coffee (shown in the figure through blue coloured hatched lines) is given by
$n\left( {I \cap T} \right) - n\left( {I \cap T \cap C} \right) = 11 \Rightarrow 15 - n\left( {I \cap T \cap C} \right) = 11 \Rightarrow n\left( {I \cap T \cap C} \right) = 15 - 11 = 4$
Number of workers purchasing only coffee and tea but not ice-cream (shown in the figure through green coloured hatched lines) is given by
$n\left( {T \cap C} \right) - n\left( {I \cap T \cap C} \right) = 4 \Rightarrow n\left( {T \cap C} \right) - 4 = 4 \Rightarrow n\left( {T \cap C} \right) = 8$
 As we know that for any three sets i.e., $C$, $I$ and $T$, we can write
$n\left( {I \cup T \cup C} \right) = n\left( I \right) + n\left( T \right) + n\left( C \right) - n\left( {I \cap T} \right) - n\left( {T \cap C} \right) - n\left( {I \cap C} \right) + n\left( {I \cap T \cap C} \right){\text{ }} \to {\text{(1)}}$
Now substituting all the values in equation (1), we get
Number of workers purchasing either ice-cream or tea or coffee is given by
$n\left( {I \cup T \cup C} \right) = 42 + 36 + 30 - 15 - 8 - 10 + 4 = 79$
Since, Number of workers who did not purchase anything is equal to the total number of workers minus the number of workers purchasing either ice-cream or tea or coffee.
\[{\text{Number of workers who did not purchase anything}} = 123 - 79 = 44\].

Note: In these types of problems, a venn diagram is used to calculate all the unknowns. In this particular problem, we used the given data to determine the unknowns in equation (1).